दी गई आकृति में l∣∣m और M, रेखाखण्ड का मध्य - बिन्दु है सिद्ध करे कि M, रेखाखण्ड CD का भी मध्य - बिन्दु है जिसके अंत बिन्दु क्रमशः l और m पर है।
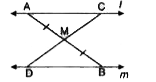
The correct Answer is:M, CD का भी मध्य - बिन्दु है।
Step by step video, text & image solution for दी गई आकृति में l||m और M, रेखाखण्ड का मध्य - बिन्दु है सिद्ध करे कि M, रेखाखण्ड CD का भी मध्य - बिन्दु है जिसके अंत बिन्दु क्रमशः l और m पर है। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुजों की सर्वांगसमता BOOK - S CHANDCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - प्रश्नावली 20.1
14 Videos
- त्रिभुजों की सर्वांगसमता BOOK - S CHANDCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - प्रश्नावली 20.2
8 Videos
- त्रिभुजों की संगामी रेखाएँBOOK - S CHANDCHAPTER - त्रिभुजों की संगामी रेखाएँEXERCISE - प्रश्नावली 23.1 (रिक्त स्थानों की पूर्ति करे) :
6 Videos
- दो चरों वाले रैखिक समीकरण BOOK - S CHANDCHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - प्रश्नावली 7.2
28 Videos
Similar Questions
यदि निम्नलिखित में से कोई भी सत्य है तो सिद्ध करें कि ΔABC एक समद्विबाहु त्रिभुज है।
∠BAC का समद्विभाजक BC पर लम्ब है
View SolutionΔABC में, ∠A=90∘,AB=AC तो ∠B और ∠C ज्ञात करें
View Solutionएक त्रिभुज की भुजाओ के लंबार्धक…………...बिन्दु से होकर जाते है।
View Solutionकोटि 0 वाले बिन्दु कहाँ पर स्थित होते है ?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि बिन्दु P(−3,4) से होकर जाने वाली एक सरल रेखा इस प्रकार है कि इसके निर्देशांक अक्षो के बीच अंत: खंडित भाग का मध्य -बिन्दु P है, तो इसका समीकरण है
View Solutionयदि बिन्दु (4, 2) का रेखा L = 0 के सापेक्ष प्रतिबिम्ब (-2, 6) है, तो L का समीकरण है
View Solution
