द्रव्यमान m के एक पिण्ड का पथ निम्न है-
x=x0+acosω1t
x=y0+bsinω2t
पर मूलबिन्दु के सापेक्ष पिण्ड पर लगने वाला जड़त्व आघूर्ण होगा।
m(−x0b−y0a)ω21ˆk
−m(x0bω22−y0aω21)ˆk
शून्य
+my0aω21ˆk
The correct Answer is:C
Step by step video, text & image solution for द्रव्यमान m के एक पिण्ड का पथ निम्न है- x =x_(0) + a cos omega_(1)t x = y_(0) + b sin omega_(2)t पर मूलबिन्दु के सापेक्ष पिण्ड पर लगने वाला जड़त्व आघूर्ण होगा। by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)EXERCISE - APRIL ATTEMPT (10 APRIL, SHIFT-II)
90 Videos
- JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)EXERCISE - JANUARY ATTEMPT (9 JAN, SHIFT -I)
30 Videos
- JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)EXERCISE - APRIL ATTEMPT (9 APRIL, SHIFT-II)
30 Videos
- JEE MAIN 2019BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019EXERCISE - JANUARY ATTEMPT (11 JAN, SHIFT-II )
30 Videos
- JEE MAIN संयुक्त प्रवेश परीक्षा सॉल्वड पेपर 2013 BOOK - ARIHANT HINDICHAPTER - JEE MAIN संयुक्त प्रवेश परीक्षा सॉल्वड पेपर 2013 EXERCISE - MCQ
30 Videos
Similar Questions
एक ग्रह की सतह से 20 किमी ऊँचाई पर एक अन्तरिक्षयान ग्रह के परित: कक्षा में घूम रहा है। यदि यान पर सिर्फ ग्रह का गुरुत्वीय क्षेत्र प्रभावी है, तो यान द्वारा 24 घण्टों में लगाए गए पूरे चक्करों की संख्या का मान होगा (दिया है, ग्रह का द्रव्यमान = 8×1022 किग्रा, ग्रह की त्रिज्या = 2×106 मी, गुरुत्वीय नियतांक, G=6.67×10−11N−m2/kg2)
View Solutionचिकनी सतह पर रखे m द्रव्यमान के एक गुटके को स्प्रिंग नियतांक की एक कमानी (जिसका द्रव्यमान नगण्य है) से जोड़ा गया है। कमानी का दूसरा सिरा चित्रानुसार अचल है। आरम्भ में गुटका अपनी साम्यावस्था में स्थायी है। यदि गुटके को एक नियत बल F से खींचा जाए, तो गुटके की अधिकतम चाल होगी-
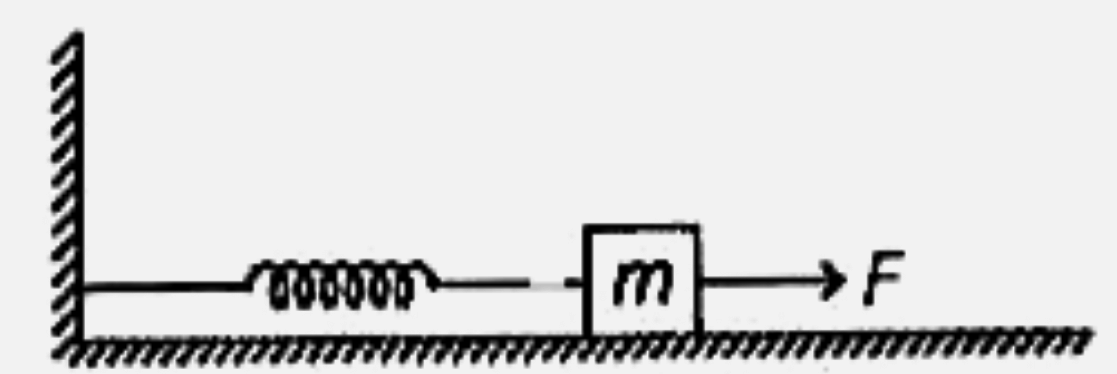
View Solution20 cm फोकस दूरी के एक उत्तल लेंस से किसी वस्तु के प्रतिबिम्ब का आवर्धन 2 ही होता, जब वस्तु को लेंस से दो दूरियों तथा x3(x1>x2) पर रखते हैं। x1 और x2 का अनुपात है-
View Solutionएक m द्रव्यमान का अल्फा कण किसी अज्ञात द्रव्यमान के स्थिर नाभिक से एक-विमीय प्रत्यास्थ संघट्ट करके अपनी प्रारम्भिक गतिज ऊर्जा का 64% भाग क्षय करके ठीक विपरीत दिशा में प्रकीर्णित हो जाता है। नाभिक का द्रव्यमान होगा
View Solutionलम्बाई L, द्रव्यमान M और अनुप्रस्थ परिच्छेद क्षेत्रफल A वाले एकसमान बेलन को इसकी लम्बाई ऊर्ध्वाधर रखते हुए एक द्रव्यमानविहीन कमानी द्वारा एक नियत बिन्दु से इस प्रकार लटकाया गया है कि साम्यावस्था की स्थिति में इसका आधा भाग घनत्व σ के द्रव में डूबा रहे। जब बेलन साम्यावस्था में है, तब कमानी में विस्तार x0 है
View SolutionThe differential equation satisfied by y=A sin(omega t+omega_(0))+B cos(omega t+omega_(0))(omega,omega_(0) are known constant) is
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View SolutionVm आयाम तथा ω0=1√LC आवृत्ति के विभव द्वारा चलित एक परिपथ अनुनादित होता है । गुणता कारण Q का मान होगा :
View Solutionदो प्रगामी तरंगों y1=A1sin(ω1t−k1x) तथा y2=A2sin(ω2t−k2x) के बीच कलान्तर क्या है ?
View SolutionIf two independent waves are y1=a1sinω1 and y2=a2sinω2t then
View Solutionनिम्न फलनों का x के सापेक्ष समाकलन कीजिए -
ex/√2cos(x+α)
View Solutionनिम्न फलनों का x के सापेक्ष अवकलन ज्ञात कीजिए
cos(x3).sin2(x5)
View Solutionयदि एक बल →F=3ˆi+2ˆj−4ˆk एक बिन्दु P(1,-1,2) पर कार्यरत है, तब बिन्दु Q(2, -1, 3) के सापेक्ष →F का आघूर्ण है
View SolutionTwo waves are expressed as, y_(1) = a sin omega_(1) ((x)/(c)-t) and y_(2) = a sin omega_(2) ((x)/(c)-t) Find the resultant displacement due to superposi-tion of the two waves .
View Solutionद्रव्यमान m के एक पिण्ड का पथ निम्न है
x=x0+acosω1t
y=y0+bsinω2t
t=0 पर, मूलबिंदु के सापेक्ष पिण्ड पर लगने वाला जड़त्व आघूर्ण होगा
View Solutionजड़त्व आघूर्ण पर महत्वपूर्ण उधारण
View Solution
