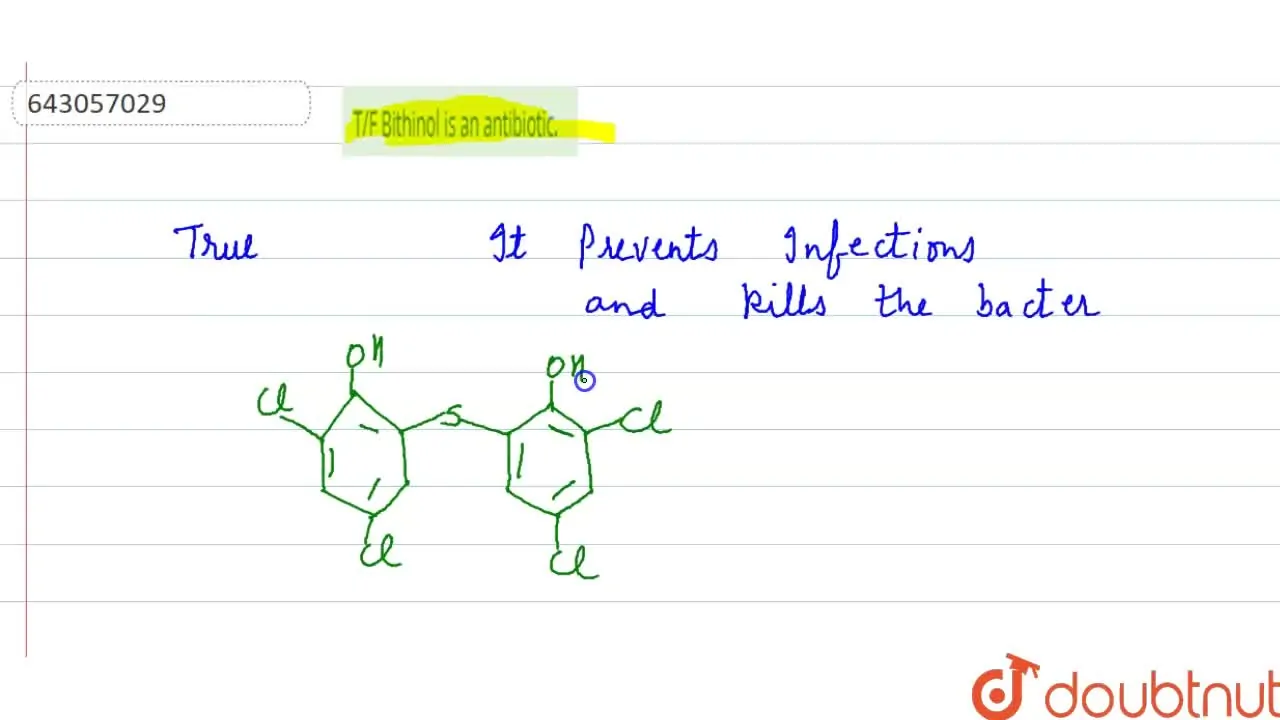
T/F Bithinol is an antibiotic.Solution in Punjabi
The correct Answer is:F
Step by step video, text & image solution for T/F Bithinol is an antibiotic. by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Which of the following 0.1 M aqueous solution will have lowest freezing point?
04:20View SolutionThe correct structure of Fe(CO)5 is
03:45View SolutionIff(y)=ey,g(y)>0,andF(t)=∫t0t(t−y)dt,then F(t)=et−(1+t) F(t)=tet F(t)=te−1 (d) F(t)=1−et(1+t)
07:59View SolutionIf =f''(t)cos t+f'(t)sin t,y=-f''(t)sin t+f'(t)cos t, then int[((dx)/(dt))^(2)+((dy)/(dt))^(2)]^((1)/(2))dt is equal to
02:35View SolutionIf int_(a)^(x)(((f(t)-f(a))/((t-a)^(2)))-((f'(a))/((t-a))))dt has no critical points,then f(x) can be
03:03View SolutionA curve is represented parametrically by the equations x=f(t)=aIn(b')andy=g(t)=b−In(at)a,b>0anda≠1,b≠1 Where t∈R.
The value of f(t)f'(t)⋅f''(−t)f'(−t)+f(−t)f'(−t)⋅f''(t)f'(t)∀t∈R is03:12View Solutionजिन अभिवयन्त्रिकी में प्रतिजैविक का उपयोग किया जाता है-
06:57View Solutionयदि f(t)=et और φ(t)=loget तो सिद्ध करें कि f{φ(t)}=φ{f(t)}.
01:05View SolutionIf x=f(t), y=g(t) possess second order derivatives for all t in (a,b) and f'(t) is invertible [f'(t)≠0], then prove that :
d2ydx2=f'(t)g''(t)−g'(t)f''(t)[f'(t)]3.03:46View SolutionIf f(t)=1−t1+t then the value of f'(1/t) is
03:52View SolutionA cure is represented parametrically by the equation x=f(t)=aIn(bt)andy=g(t)=b−In(at)a,b>0anda=≠1,b≠1 where t∈R
The value of f(t)f'(t).f''(−t)f'(−t)+f(−t)f'(t).f''(t)f''(t)∀t∈R is equal to01:51View SolutionMention whether the following statements are true (T) or false (F) Foods protect us from disease and therefore antibiotics which protect us from disease are also foods. (T/F) " "...............
02:12View SolutionMention if the following statements are true (T) or false (F). Lysol is an antibiotic.
04:43View SolutionMention if the following statements are true (T) or false (F).
Alexander Fleming coined the term "antibiotic" for substances like penicillin.01:46View SolutionA particle moving on a curve has the position at time t given by x=f'(t)sint+f''(t)cost,y=f'(t)cost−f''(t)sint where f is a thrice differentiable function. Then prove that the velocity of the particle at time t is f'(t)+f'''(t).
05:12View Solution