एक त्रिभुज में दो न्यूनकोण हो सकते है।
The correct Answer is:सत्य
Step by step video, text & image solution for एक त्रिभुज में दो न्यूनकोण हो सकते है। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज Book:S CHANDChapter:त्रिभुज Exercise:प्रश्नावली 18.2
Explore 8 Videos
- त्रिभुज Book:S CHANDChapter:त्रिभुज Exercise:प्रश्नावली 18.2 रिक्त स्थानों को भरे :
Explore 5 Videos
- त्रिभुज Book:S CHANDChapter:त्रिभुज Exercise:प्रश्नावली 18.1 रिक्त स्थानों को भरे:
Explore 7 Videos
- त्रिकोणमितीय Book:S CHANDChapter:त्रिकोणमितीय Exercise:प्रश्नावली 27.3
Explore 11 Videos
- त्रिभुज में असमिकाएँ Book:S CHANDChapter:त्रिभुज में असमिकाएँ Exercise: प्रश्नावली 21. 8
Explore 1 Video
Similar Questions
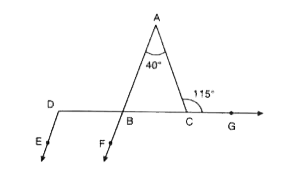
आकृति में, सिद्ध कीजिये कि DE∣∣BF
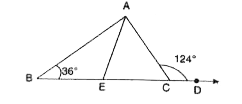
View Solutionयदि ∠ACD=124∘,∠ABC=36∘, तो ∠BAC=………….
View Solutionत्रिभुज के तीनो कोणों का योग……. है।
View Solutionत्रिभुज ABC में कोण B समकोण है। त्रिभुज के शेष अवयव ज्ञात कीजिए यदि :
∠C=45∘,AB=5 सेमी
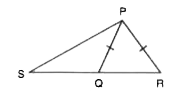
View Solutionआकृति में, PQ = PR, तो सिद्ध करें कि PS>PQ
View Solutionशनि के और भी कुछ चंद्र हो सकते है।
View Solutionएक त्रिभुज OAC में यदि B भुजा AC का मध्य-बिंदु हो तथा −−→OA=¯a,−−→OB=¯b, तब सदिश −−→OC क्या है?
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक त्रिभुज की दो भुजाओं की मापों का योग
View Solutionएक त्रिभुज की रचना|जब दो कोण एवं तीनों भुजाओं का योग दिया हो
View Solutionयदि दो समकोण त्रिभुजों में से एक त्रिभुज की एक भुजा और एक न्यूनकोण दूसरे त्रिभुज की एक भुजा और तदनुरूपी कोण के बराबर हो, तो दोनों त्रिभुज परस्पर क्या होंगे ?
View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
View Solutionक्या परिवर्तन करने के अन्य तरीके हो सकते है
View Solutionक्या परिवर्तन करने के अन्य तरीके भी हो सकते है
View SolutionIn an equilateral triangle, the value of each exterior angle is: एक समबाह त्रिभुज में, प्रत्येक बाहरी कोण का मान है:
View Solutionत्रिभुज#!#त्रिभुज : एक परिचय
View Solution
