यदि एक अचर त्रिज्या 3k का वृत्त मूल बिन्दु से गुजरता है एवं अक्षों को A व B पर मिलता है, तो त्रिभुज OAB के केन्द्रक का बिन्दुपथ है
The correct Answer is:A
Step by step video, text & image solution for यदि एक अचर त्रिज्या 3k का वृत्त मूल बिन्दु से गुजरता है एवं अक्षों को A व B पर मिलता है, तो त्रिभुज OAB के केन्द्रक का बिन्दुपथ है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- वृतBOOK - BANSAL HINDICHAPTER - वृतEXERCISE - EXERCISE - 1 (SPECIAL DPP - 9)
11 Videos
- वृतBOOK - BANSAL HINDICHAPTER - वृतEXERCISE - EXERCISE - 1 (SPECIAL DPP - 10)
11 Videos
- वृतBOOK - BANSAL HINDICHAPTER - वृतEXERCISE - EXERCISE - 1 (SPECIAL DPP - 7)
10 Videos
- फलन की सीमा सत्त्यता तथा अवकलनीयता BOOK - BANSAL HINDICHAPTER - फलन की सीमा सत्त्यता तथा अवकलनीयता EXERCISE - Exercise -5 (Rank Booster)
5 Videos
- सदिश एवं त्रिविम निर्देशांक ज्यामितीय (VECTOR & 3-D)BOOK - BANSAL HINDICHAPTER - सदिश एवं त्रिविम निर्देशांक ज्यामितीय (VECTOR & 3-D)EXERCISE - EXERCISE-5 (RANK BOOSTER)
13 Videos
Similar Questions
केन्देर (2, 3) तथा (5, 6) वाले दो सर्वांगसम वृत एक दूसरे को समकोण पर काटते है तो वृतों की त्रिज्या होगी
View Solutionवृत x2+y2=1 की उस जीवा के मध्य बिंदु का बिन्दुपथ, जो इस प्रकार है की परवलय y=x2−x पर जीवा का खण्ड मूल बिंदु पर समकोण अंतरित करें एक वृत है जिसका केंद्र तथा त्रिज्या क्रमशः है
View Solutionउस वृत के केंद्र का बिन्दुपथ, जो की वृत x2+y2−6x−6y+14=0 को बाह्य स्पर्श करता है तथा y- अक्ष को भी स्पर्श करता है, होगा
View Solutionयदि l=Limn→∞n∑r=2((r+1)sinπr+1−rsinπr) है, तो {l} मान ज्ञात करो। (जहाँ पर {} भिन्नात्मक भाग फलन है)
View Solutionकिसी चतुष्फलक के शीर्ष A,B,C की स्थिति सदिश क्रमशः (1,1,1),(1,0,0) तथा (3,0,0) है। यदि शीर्ष D से विपरीत तल ABC पर लंब डाला जाता है तथा यह त्रिभुज ABC के शीर्ष A से जाने वाली माध्यिका पर बिंदु E पर मिलता है। यदि AD की लम्बाई 4 तथा चतुष्फलक का आयतन 2√23 है। तो E की स्थिति ज्ञात कीजिए।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
View Solutionनिम्नलिखित स्थितियों में एक चर बिंदु का बिन्दुपथ ज्ञात कीजिए जिसकी
दोनों अक्षों से दूरियों का योग एक अचर राशिc है ।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
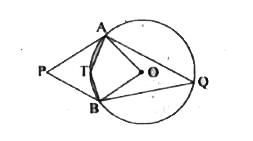
View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
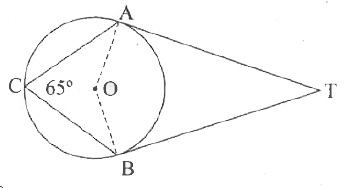
View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक बिंदु P,2x−3y+4=0 पर गति करता है । यदि Q(1,4) तथा R(3,-2) निश्चित बिंदु है, तो ΔPQR के केन्द्रक का बिन्दुपथ (locus) एक रेखा है
View Solution
