दो नाभिकों pn और Q2n को बन्धन ऊर्जा क्रमशः x जूल और y जूल हैं। यदि 2x>y , तब अभिक्रिया pn+pn=Q2n में निकलने वाली ऊर्जा होगी
2x+y
2x−y
xy
x+y
The correct Answer is:b
मुक्त ऊर्जा = प्रारम्भिक BE - अंतिम BE=2x−y
Topper's Solved these Questions
- परमाणवीय एवं नाभिकीय भौतिकीBook:ARIHANT HINDIChapter:परमाणवीय एवं नाभिकीय भौतिकीExercise:प्रश्नावली - स्तर 2
Explore 75 Videos
- परमाणवीय एवं नाभिकीय भौतिकीBook:ARIHANT HINDIChapter:परमाणवीय एवं नाभिकीय भौतिकीExercise:प्रश्नावली - स्तर 2 (विगत वर्षों के प्रश्न )
Explore 31 Videos
- परमाणवीय एवं नाभिकीय भौतिकीBook:ARIHANT HINDIChapter:परमाणवीय एवं नाभिकीय भौतिकीExercise:प्रश्नावली - स्तर 2 (विगत वर्षों के प्रश्न )
Explore 31 Videos
- पदार्थ की द्वैती प्रकृति एवं विकिरण Book:ARIHANT HINDIChapter:पदार्थ की द्वैती प्रकृति एवं विकिरण Exercise:प्रश्नावली स्तर 2 (विगत वर्षों के प्रश्न)
Explore 8 Videos
- परमाणवीय भौतिकी Book:ARIHANT HINDIChapter:परमाणवीय भौतिकी Exercise:विगत वर्षो के प्रश्न
Explore 13 Videos
Similar Questions
शीतलक नलिका से X-किरणों की तीव्रता λतरंगदैर्ध्य के विपरीत है जैसा कि चित्र में दिखाया गया है। न्यूनतम तरंगदैर्ध्य λc प्राप्त होती है तथा Kα रेखा की तरंगदैर्ध्य λKहै। चूँकि त्वरित विभव बढ़ता है
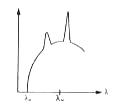
View Solutionद्रव्यमान nN (संवेग ~0) के धीमी गति के न्यूट्रॉन को ग्रहण करने के बाद, द्रव्यमान M का नाभिक क्रमश: m1 तथा 5m1(6m1=M+mN) के दो न्युक्लिआइ में टूट जाता है। यदि नाभिक का द्रव्यमान m1 के साथ दे- ब्रोग्ली तरंगदैर्ध्य λ है, तब नाभिक की दूसरे के साथ तरंगदैर्ध्य होगी
View Solutionद्रव्यमान nN (संवेग ~0) के धीमी गति के न्यूट्रॉन को ग्रहण करने के बाद, द्रव्यमान M का नाभिक क्रमश: m1 तथा 5m1(6m1=M+mN) के दो न्युक्लिआइ में टूट जाता है। यदि नाभिक का द्रव्यमान m1 के साथ दे- ब्रोग्ली तरंगदैर्ध्य λ है, तब नाभिक की दूसरे के साथ तरंगदैर्ध्य होगी
View Solutionλ तरंगदैर्ध्य का प्रकाश, ऐसी धातु पर गिरता है जिसका कार्य फलन hcλ0 है, प्रकाश वैघुत प्रभाग उत्पन्न होगा, यदि
View SolutionLi++ के लिए पहले से तीसरे बोर कक्ष में इलेक्ट्रॉन उत्तेजन के लिए आवश्यक ऊर्जा है
View SolutionIn the expansion of (x+a)n if the sum of odd terms is P and the sum of even terms is Q, then (a)P2−Q2=(x2−a2)n (b)4PQ=(x+a)2n−(x−a)2n (c)2(P2+Q2)=(x+a)2n+(x−a)2n (d)none of these
View SolutionLet the co-efficients of x^(n) In (1+x)^(2n) and (1+x)^(2n-1) be P& Qrespectively,then ((P+Q)/(Q))^(5)=
View SolutionLet w is non-real root of x^3 =1 (i) If P = w^n, (n in N) and Q = (.^(2n)C_0 + .^(2n)C_3 +.....)+( .^(2n)C_1 + .^(2n) C_4+.....)w + (.^(2n)C_2 + .^(2n)C_2+.^(2n)C_5+....)w^2 then find P/Q
View SolutionThe binding energies of two nuclei Pn and Q2n and x and y joules. If 2x>y then the energy released in the reaction Pn+Pn→Q2n, will be
View Solutionif f(x) =∣∣ ∣ ∣∣mxmx−pmx−pnn+pn−pmx+2nmx+2n+pmx+2n−p∣∣ ∣ ∣∣ then
y=f(x) represents
View Solution(A)नाभिकों Xn तथा Y2n की बंधन ऊर्जायें क्रमशः P तथा Q जूल प्रति न्यूक्लिऑन हैं। यदि 2P<Q हो तो नाभिकीय अभिक्रिया Xn+Xn→Y2n में उत्सर्जित ऊर्जा ज्ञात कीजिए।
(B) एक नाभिक Xn की बंधन ऊॅर्जा P तथा दूसरे नाभिक Y2n की बंधन ऊर्जा Q है। n तथा 2n नाभिकों की द्रव्यमान संख्यायें हैं। यदि 2P>Q हो तो अभिक्रिया Xn+Xn→Y2n में ऊर्जा मुक्त होगी अथवा अवशोषित?
View Solutionमाना R3 में p, q और r तीन असमतलीय सदिश हैं। माना सदिश s के घटक क्रमागत सदिशों p, q एवंr के अनुदिश क्रमशः 4, 3 और 5 हैं। यदि s के घटक क्रमागत सदिशों (−p+q+r),(p−q+r) एवं (−p−q+r) के अनुदिश क्रमशः x,y और z हैं, तब 2x+y+z का मान है।
View Solutionयदि x और y दो वास्तविक संख्याएँ है और m व n धन पूर्णाक है, तब xnym(1+x2n)(1+y2m)>14
View Solutionदो नाभिको Pn व Q2n की बंधन ऊर्जा क्रमशः x जूल व y जूल है। यदि 2x>y, तो क्रिया Pn+Pn=Q2n में मुक्त ऊर्जा होगी
View SolutionIn the expansion of (x+a)n if the sum of odd terms is P and the sum of even terms is Q, then (a)P2−Q2=(x2−a2)n (b)4PQ=(x+a)2n−(x−a)2n (c)2(P2+Q2)=(x+a)2n+(x−a)2n (d)none of these
View SolutionIf P(n) :2n<n!,n∈N , then P(n) is true for all n≥…………...
View Solution

