Observe the following diagram and answer the questions:
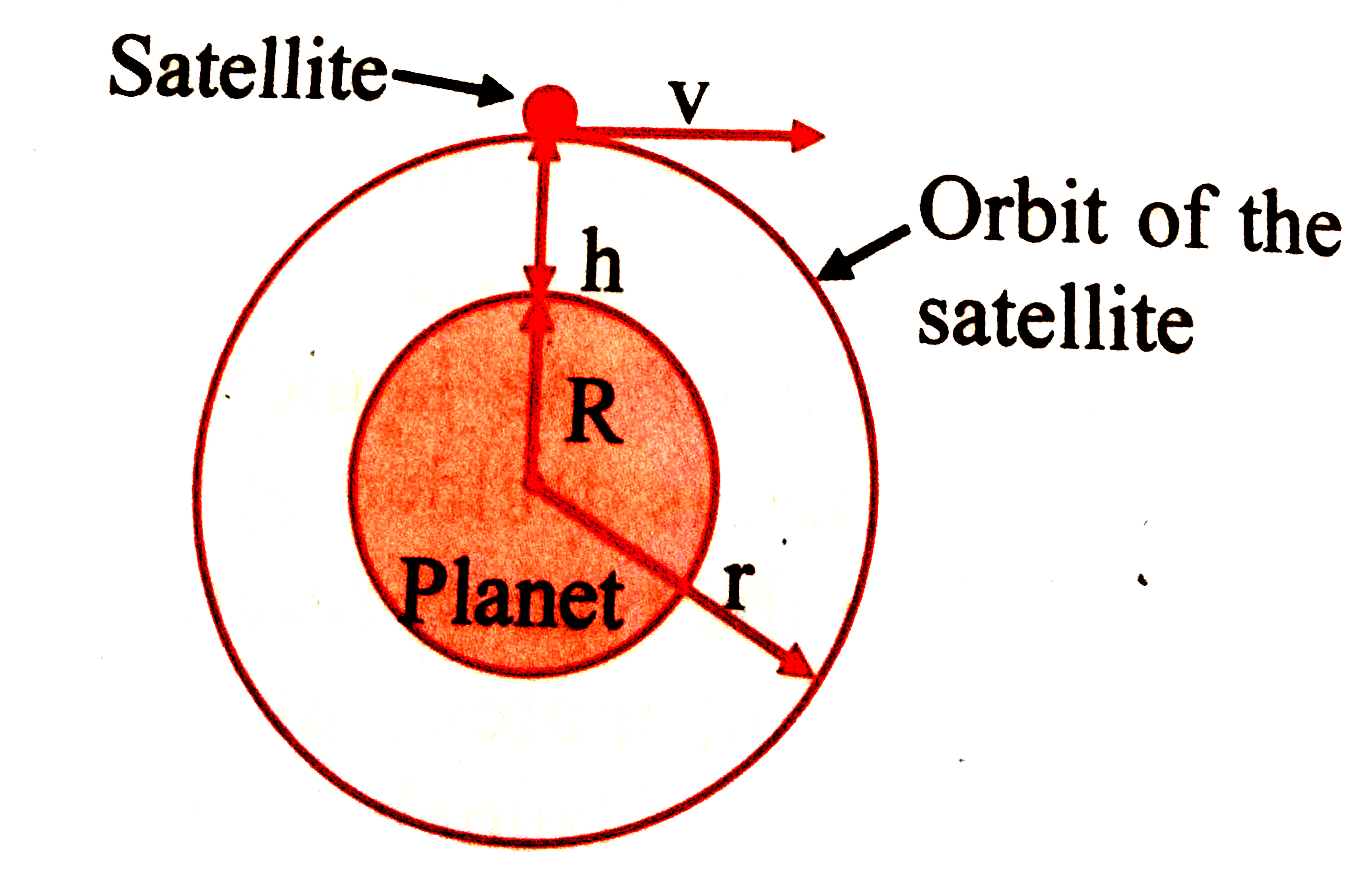
Derive the formula for that velocity of satellite assuming the mass of the planet M and mass of satellite as m .Solution in Marathi
Critical velocity of a satellite revolving around the planet in circular orbit can be derived as follows: Consider the satellite of mass m revolving at height around the planet of mass M and radius above . As the satellite is moving in circular orbit, centripetal force acting on it is provided by the gravitational force of the planet,
i e . , mv2r=GMmr2
But r =R+h
∴ v2=GM(R+h)
∴ v=√GMR+h
Hence , critical velocity is given by formula
√GMR+h.
Similar Questions
Orbital velocity of a satellite around a planet is independent of the mass of the ____ but depends on the mass of the .
View SolutionA wreckage of mass m present in space collides with a satellite of mass 10m and orbital radius R as shown. As a result of collision, the wreckage sticks to the satellite and the satellite is transferred to an orbit whose minimum distance from the planet is R/2. If mass of planet is M, with what velocity the wreckage collided the satellite?

View SolutionA satellite with mass m is located at a distance r from the center of the earth (mass M). Satellite's mechanical energy is
View SolutionAn artificial satellite of mass m is orbiting around the earth of mass M in an orbit of radius R, with a constant angular velocity. What is the angular momentum of a satellite ?
View SolutionIf r represents the radius of the orbit of a satellite of mass m moving round a planet of mass M, the velocity of the satellite is given by :
View SolutionA satellite of mass 'm' is revolving in a circular orbit of radius 'r' around the earth of mass M. What is the total energy of the satellite?
View SolutionA satellite of mass m revolves in a circular orbit of radius R a round a planet of mass M. Its total energy E is :-
View Solution

