एक टैंक में H1 ऊँचाई पर द्रव भरा है। टैंक का परिच्छेद क्षेत्रफल A है। टैंक की तली में a परिच्छेद का एक छिद्र किया गया है। टैंक में द्रव के तल को H1 ऊँचाई से H2 ऊँचाई तक गिरने में कितना समय लगेगा?
dt समय में बहने वाले द्रव का आयतन,
dV=av×dt=a√2gHdt
(यदि dt समय में तल dH नीचे गिरता है।)
अत: बाहर निकले द्रव का आयतन dV=A(−dH)
A=(−dH)=a√2gHdt
या dt=−Aa√2g×dH(H)1/2
अत: द्रव तल के H1 ऊँचाई से H2 ऊँचाई तक गिरने में लगा समय,

∫t0dt=−Aa√2g∫H2H1(H)−1/2dH
या t=−Aa√2g(H1/21/2)H2H1=Aa√2g×(√H1−√H2)
Topper's Solved these Questions
- द्रवों के गुण BOOK - ARIHANT HINDICHAPTER - द्रवों के गुण EXERCISE - साधित उदाहरण
12 Videos
- द्रवों के गुण BOOK - ARIHANT HINDICHAPTER - द्रवों के गुण EXERCISE - प्रारम्भिक प्रश्नावली 1
5 Videos
- द्रव व ठोसों के गुणBOOK - ARIHANT HINDICHAPTER - द्रव व ठोसों के गुणEXERCISE - प्रश्नावली (विगत वर्ष के प्रश्न)
20 Videos
- द्रव्यमान केंद्रBOOK - ARIHANT HINDICHAPTER - द्रव्यमान केंद्रEXERCISE - प्रश्नवली (विगत वर्षों के प्रश्न)
7 Videos
Similar Questions
चित्र में दिखायी गयी व्यवस्था के लिये तेल का घनत्व ज्ञात कीजिए।
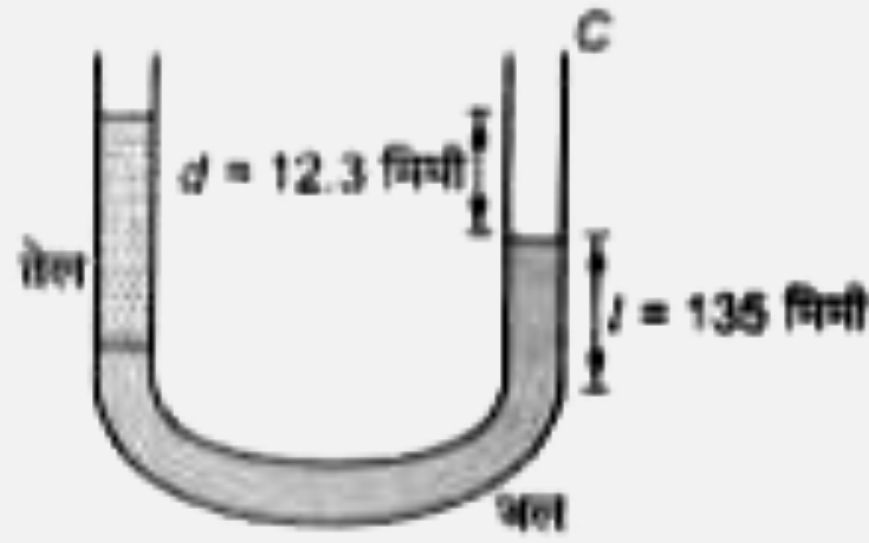
View Solutionकॉर्क के एक छोटे तथा एक बड़े टुकड़े को पानी के तल पर नीचे की ओर धकेलते हैं कौन-सा टुकड़ा नीचे की ओर तीव्र गति से जायेगा?
View Solutionएक U आकार के तार एवं हल्के दर्पण के बीच बनी एक पतली द्रव की फिल्म 1.5×10−2 न्यूटन के भार को आधारित करती है( चित्र में देखने) दर्पण की लम्बाई 30 सेमी है ओर इसका भार नगण्य है। द्रव की फिल्म का पृष्ट तनाव है।
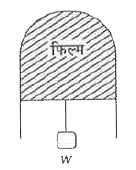
View Solutionα कोण पर झुके नत समतल पर एक ठोस डिस्क नीचे की ओन लुढ़क रही है इसके द्रव्यमान केंद्र का त्वरण होगा
View SolutionA tank can be filled by pipe A in 5 hours and emptied by pipe B in 8 hours respectively. How much time will it take for the tank to be half full?
एक टैंक को पाइप A द्वारा 5 घंटे में भरा जा सकता है और पाइप B द्वारा क्रमशः 8 घंटे में खाली किया जा सकता है। टैंक को आधा भरा होने में कितना समय लगेगा?
View SolutionA pipe can fill a tank in 32 minutes. Due to a leak the tank is filled in 48 minutes. How long will it take to empty the tank due to leakage?
एक पाइप 32 मिनट में एक टैंक भर सकता है | रिसाव के कारण टैंक 48 मिनट में भर पाता है | रिसाव के कारण भरा हुआ टैंक खाली होने में कितना समय लगेगा ?
View SolutionPipe P can fill a tank alone in 7 hours. Pipe Q can fill the same tank alone in 13 hours. In how much time can they together fill the tank?
पाइप P, 7 घंटे में अकेले एक टैंक भर सकता है। पाइप Q उसी टैंक को 13 घंटे में भर सकता है। वे एक साथ कितने में टैंक को भर सकते है?
View SolutionPipe A can fill a tank in 36 minutes and pipe B is able to empty this in 45 minutes. If both pipes are opened simultaneously, then the tank will filled half in _______hours.
पाइप A किसी टैंक को 36 मिनट में भर सकता है। और पाइप B उसे 45 मिनट में खाली कर सकता है। यदि दोनों पाइपों को एक साथ खोल दिया है, तो टैंक की आधी क्षमता को भरने में लगने वाला समय (घंटो में) है:
View SolutionA pipe can fill a tank in 18 hours. In how much time (in hours) will another pipe operating at one-third the efficiency of the first pipe fill a tank whose capacity is 50% of that of the first tank?
एक पाइप 18 घंटे में एक टैंक भर सकता है। कितने समय में (घंटों में) पहले पाइप की एक तिहाई कार्य कुशलता पर चलने वाला दूसरा पाइप उस टैंक को भर देगा जिसकी धारिता पहले टैंक की तुलना में 50% है?
View SolutionA pipe can fill a tank in 56 hours, but due to leakage in its base, it takes 16 hours more to fill it. Only in how much time (in hours) can the 8313% portion of the leakage tank be consumed? /
एक पाइप 56 घंटे में किसी टैंक को भर सकता है, लेकिन इसकी तली में रिसाव के कारण उसे भरने में 16 घंटे अधिक लगते है। मात्र रिसाव के कारण टैंक के 8313% हिस्से को कितने समय (घंटों में) में खाली कर सकता है|
View SolutionTap A can fill a tank in 6 hours, tap B can fill the same task in 8 hours and tap C can empty the same tank in 4 hours. If all three taps A, B and C are opened together, then how much time (in hours) will be taken to fill the tank?
टैप A 6 घंटे में एक टैंक भर सकता है, टैप B उसी टैंक को 8 घंटे में भर सकता है और C उसी टैंक को 4 घंटे में खाली कर सकता है। यदि सभी तीन टैप A, B और C को एक साथ खोला जाता है, तो टैंक को भरने में कितना समय (घंटों में) लगेगा?
View SolutionTap A can fill a tank in 20 hours and tap B can fill the same tank in 30 hours. If both taps are opened together, then how much time will be taken to fill the tank?
टैप A 20 घंटे में एक टैंक भर सकता है और टैप B 30 घंटे में एक ही टैंक भर सकता है। यदि दोनों नल एक साथ खोले जाते हैं, तो टैंक को भरने में कितना समय लगेगा?
View SolutionTap A can fill a tank in 6 hours and tap B can empty the same tank in 10 hours. If both taps are opened together, then how much time (in hours) will be taken to fill the tank?
नल A, 6 घंटे में एक टैंक भर सकता है और नल B,10 घंटे में उसी टैंक को खाली कर सकता है। यदि दोनों नल एक साथ खोले जाते हैं, तो टैंक को भरने में कितना समय (घंटों में) लगेगा?
View SolutionA hemispherical tank full of water is emptied by a pipe at the rate of 7.7 liters per seconds. How much time(in hours) will it take to empty 2/3 part of the tank if the internal radius of the tank is 10.5 m ? पानी से भरा एक गोलार्ध टैंक 7.7 लीटर प्रति सेकेंड की दर से एक पाइप द्वारा खाली किया जाता है। टैंक के 2/3 हिस्से को खाली करने में कितना समय लगेगा(घंटे में), यदि टैंक की आंतरिक त्रिज्या 10.5 मीटर है?
View SolutionA pipe can fill a leak-proof tank completely in 24 hours. A leakage at the midpoint of the same size tank empties half the tank in 36 hours. How much time will it take to fill this tank with the given pipe?
एक नली एक रिवास रहित टैंक को 24 घंटे में भरती है | समान आकार के टैंक जिसमें मध्य में छेद है आधे पानी को 36 घंटे में खाली करता है | दी गयी नली से टैंक को भरने में कितना समय लगेगा ?
View SolutionA tap fills up a tank of 1250 litres in 4 hours, whereas another tap can fill the same tank in 8 hours. An outlet tap can empty that tank in 6 hours. If all the three taps are opened simultaneously, then how much time will it take to fill the tank completely? एक नल 4 घंटे में 1250 लीटर का टैंक भरता है, जबकि दूसरा नल उसी टैंक को 8 घंटे में भर सकता है। एक आउटलेट नल 6 घंटे में उस टैंक को खाली कर सकता है। यदि सभी तीन नल एक साथ खोले जाते हैं, तो टैंक को पूरी तरह से भरने में कितना समय लगेगा?
View Solution
