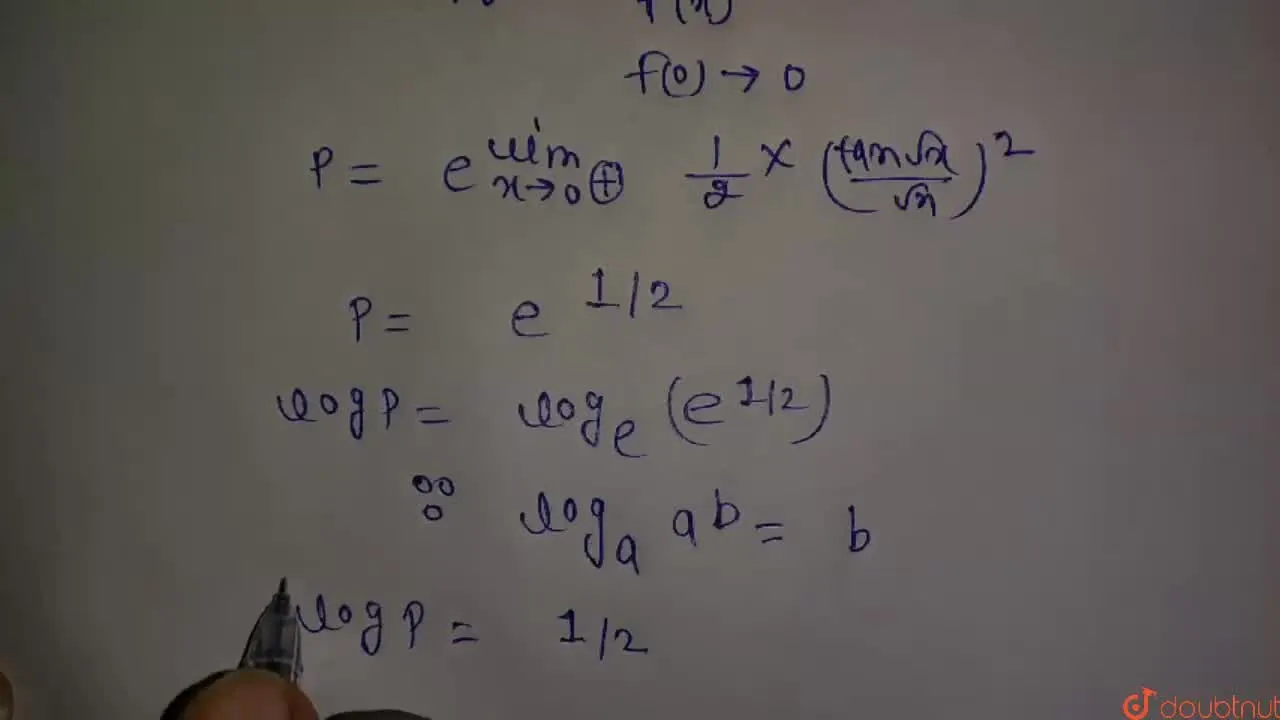माना ρ=limx→0+(1+tan2√x)12x है, तो logρ बराबर है
2
1
12
14
The correct Answer is:C
Step by step video, text & image solution for माना rho = underset(xto0^(+))("lim")(1+tan^2 sqrtx)^(1/(2x)) है, तो log rho बराबर है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
यदि λ के उन सभी वास्तविक मानो, जिनके लिए बिन्दुओ (−λ2,1,1),(1,−λ2,1) तथा (1,1,−λ2) से होकर जाने वाला एक समतल, बिंदु (-1, -1, 1) से भी होकर जाता है, का समुच्चय S है, तो S बराबर है
02:03View SolutionEvaluate :limx→0√(1+sin3x)−1ln(1+tan2x)
02:31View Solutionlimx→−∞3|x|−x|x|−2x−limx→0log(1+x3)sin3x=
02:34View SolutionLet p=limx→0+(1+tan2√x)12x then log p is equal to
06:12View Solutionमाना ω एक सम्मिश्र संख्या ऐसी है कि 2ω+1=z जहाँ, z=√−3 है। यदि ∣∣ ∣ ∣∣1111−ω2−1ω21ω2ω2∣∣ ∣ ∣∣=3k है तो k बराबर है
05:05View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
02:08View Solutionमाना a1,a2,…,a10 एक गुणोत्तर श्रेढ़ी है। यदि a3a1=25, तो a9a5 बराबर है
03:35View Solutionयदि ∫(x+1)√2x−1dx=f(x)√2x−1+C है, जहाँ C एक समाकलन अचर है, तो f(x) बराबर है
04:36View Solutionlimx→0xcot(4x)sin2xcot2(2x) बराबर है
04:46View Solutionयदि x>1 के लिए (2x)2y=4e2x−2y है, तो (1+loge2x)2dydx बराबर है
03:38View Solutionमाना Sk=1+2+3+…+kk है। यदि S21+S22+….S210=512A है, तो A बराबर है
03:56View Solutionlimx→1−√π−√2sin−1x√1−x बराबर है
09:03View SolutionLet a=limx→0ln(cos2x)3x2,b=limx→0sin22xx(1−ex),c=limx→1√x−xlnx. Then a,b,c satisfy :
01:47View Solution3tan−1a बराबर है
03:59View SolutionFind the limits:
(a) limx→0arccos(1−x)√x (b) limx→π/4lntanx1−cotx
(c ) limx→01sinxln(1+asinx)07:01View SolutionLet a=limx→0ln(cos2x)3x2,b=limx→0sin22xx(1−ex),c=limx→1√x−xlnx. Then a,b,c satisfy :
01:19View Solution