माना f एक फलन है जो निम्न प्रकार से परिभाषित है f:(0,e−32]→[−14,∞),f(x)=(lnx)2+3lnx+2, तो f−1(x) बराबर है :
(i) log(−3+√4x+12)
(ii) log(−3−√4x+12)
(iii) e−3+√4x+12
(iv) e−3−√4x+12
log(−3+√4x+12)
log(−3−√4x+12)
e−3+√4x+12
e−3−√4x+12
The correct Answer is:D
Step by step video, text & image solution for माना f एक फलन है जो निम्न प्रकार से परिभाषित है f:(0,e^((-3)/(2))]to[(-1)/(4),oo),f(x)=(lnx)^(2)+3lnx+2, तो f^(-1)(x) बराबर है : (i) log((-3+sqrt(4x+1))/(2)) (ii) log((-3-sqrt(4x+1))/(2)) (iii) e^((-3+sqrt(4x+1))/(2)) (iv) e^((-3-sqrt(4x+1))/(2)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RELATION & FUNCTION BOOK - BANSAL HINDICHAPTER - RELATION & FUNCTION EXERCISE - EXERCISE - 1 (SPECIAL DPP - 5 )
9 Videos
- RELATION & FUNCTION BOOK - BANSAL HINDICHAPTER - RELATION & FUNCTION EXERCISE - EXERCISE - 1 (SPECIAL DPP - 6)
10 Videos
- RELATION & FUNCTION BOOK - BANSAL HINDICHAPTER - RELATION & FUNCTION EXERCISE - EXERCISE - 1 (SPECIAL DPP - 3 )
10 Videos
- QUADRATIC EQUATIONBOOK - BANSAL HINDICHAPTER - QUADRATIC EQUATIONEXERCISE - Exercise - 5 (Rank Booster)
11 Videos
- SOLUTION OF TRIANGLE BOOK - BANSAL HINDICHAPTER - SOLUTION OF TRIANGLE EXERCISE - EXERCISE - 5 (Rank Booster)
5 Videos
Similar Questions
y=g(x) का आरेख दर्शाया गया है तो समीकरण के ||g(x)|−1|=12 के हलो की संख्या होगी -
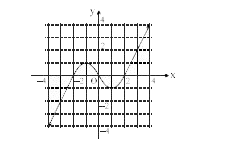
View Solutionयदि समीकरण (p2−4)(p2−9)x3+[p−22](x2+p−4)+(p2−5p+6)x+{2p−1}=0 अन्तराल (0,x) के सभी मानों द्वारा संतुष्ट होती है, तो 'p' के सभी संभव पूर्णांक मानो का योगफल है
{y} तथा [y] क्रमशः y के भिन्नात्मक भाग फलन एवं महत्तम पूर्णांक फलन को निरूपित करते है ]
View Solutionमाना F(x)=⎡⎢ ⎢⎣x|x| यदि x≤−1[1+x]+[1−x] यदि −1<x<1−x|x| यदि x≥1
जहाँ [x] महत्तम पूर्णांक फलन है तो F(x) है
View Solutionएक द्विघात बहुपद f(x)=x2+ax+b इस प्रकार है कि इसका एक शून्य 4+3√32+√3 है, जहाँ a तथा b पूर्णांक है। साथ ही, g(x)=x4+2x3−10x2+4x−10 एक चतुर्थघातीय बहुपद इस प्रकार है कि g(4+3√32+√3)=c√3+d है, जहाँ c तथा d भी पूर्णांक है। a, b, c एवं d के मान ज्ञात कीजिये।
View Solutionएक समकोणीय त्रिभुज ABC में ∠A=90∘ है माना M भुजा BC का मध्य - बिन्दु है यदि त्रिभुज ABM तथा त्रिभुज ACM के अन्तःवृत्त की त्रिज्याएँ क्रमशः r1 एवं r2 हो तो r1/r2 के मानों का परिसर ज्ञात कीजिए।
View SolutionThe domain of the function f(x)=√log(|x|−1)(x2+4x+4) is (a) (−3,−1)∪(1,2) (b)(−2,−1)∪(2,∞) (c)(−∞,−3)∪(−2,−1)∪(2,∞) (d)none of these
View Solutionf(x)=sqrt(4x-x^(2)-3)
View SolutionThe domain and range of real function f if (i) f(x)=sqrt(1-x^(2))(ii)sqrt((x-1)(x-3))(iii)sqrt(4x-x^(2)-3)
View SolutionIf x is a solution of the equation sqrt(2x+1)-sqrt(2x-1)=1(x>=(1)/(2)) then sqrt(4x^(2)-1)=( i) (3)/(4)( ii) (1)/(2)( iii) 2 (iv) 2sqrt(2)
View SolutionIf f(x)=(e^(2x)-(1+4x)^(1/2))/(ln(1-x^(2))) for x!=0, then f has
View Solution0.7Let fbe a function defined as(x) = (In x)2 + 3 In x +2 then f-'(x) equalsf:/-3+ 4x +1(2) 1086-3xxXXXBlog -3-Y4x+1)-3-248+1(B) log(A) log-3+1 4x+12-3-4x+1(D) e(C) e
View SolutionIf f(x)=√1tan−1(x2−4x+3), then f(x) is continuous for
View Solutionf(x)=√−x2+4x−3+√sinπ2(sinπ2(x−1))
View SolutionIf f(x)=tan−1√x2+4x +sin−1√x2+4x+1
View Solutionयदि ∫(x+1)√2x−1dx=f(x)√2x−1+C है, जहाँ C एक समाकलन अचर है, तो f(x) बराबर है
View SolutionThe function f:A→R,f(x)=1√4x2−1+ln(x(x2−1)), f:A→R,f(x)=1√4x2−1+ln(x(x2−1)) is (Here A is the largest possible domain of the given function
View Solution
