समीकरणों x3+4x3+px+q=0 एवं x3+6x2+px+r=0 के दो मूल उभयनिष्ठ है, जहाँ p,q,r∈R है। यदि इनके जो मूल उभयनिष्ठ नहीं है, वो समीकरण x2+2ax+8c=0 के मूल है, तो
a + c = 8
a + c = 2
3q = 2r
3r = 2q
The correct Answer is:A, C
Step by step video, text & image solution for समीकरणों x^(3) +4x^3+px + q = 0 एवं x^(3) + 6x^(2) + px + r = 0 के दो मूल उभयनिष्ठ है, जहाँ p, q, r in R है। यदि इनके जो मूल उभयनिष्ठ नहीं है, वो समीकरण x^(2) + 2a x + 8c = 0 के मूल है, तो by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRATIC EQUATIONBOOK - BANSAL HINDICHAPTER - QUADRATIC EQUATIONEXERCISE - Exercise - 1 [Special Dpp 4]
5 Videos
- QUADRATIC EQUATIONBOOK - BANSAL HINDICHAPTER - QUADRATIC EQUATIONEXERCISE - Exercise - 1 [Special Dpp 4] (Paragraph)
5 Videos
- QUADRATIC EQUATIONBOOK - BANSAL HINDICHAPTER - QUADRATIC EQUATIONEXERCISE - Exercise - 1 [Special Dpp 2 ]
10 Videos
- PROBABILITYBOOK - BANSAL HINDICHAPTER - PROBABILITYEXERCISE - EXERCISE-5 (RANK BOOSTER)
11 Videos
- RELATION & FUNCTION BOOK - BANSAL HINDICHAPTER - RELATION & FUNCTION EXERCISE - EXERCISE - 5 (Rank Booster)
16 Videos
Similar Questions
यदि x∈R है, f(x) = x2+2x−32x2+3x−9 तो का परिसर है
View SolutionP(t)=t2+4t+10t2+4t+5,t∈R एवं Q(x)=x2−2mx+6m−41 पर विचार कीजिये। जहाँ x,m∈R
P(t) के परिसर में सभी पूर्णांक मानों का योग्य है
View Solutionएक द्विघात बहुपद y=px2−qx+r का आरेख संलग्न चित्रानुसार है, तो
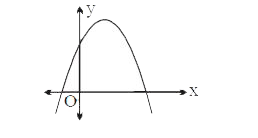
View Solution4 स्वतन्त्र प्रयासों पर विचार कीजिए जिनमें एक एक घटना A के घटित होने की प्रायिकता 13 है। यदि घटना A कम से कम दो बार घटित होती है तो घटना B के घटित होने की प्रायिकता 1 है। यदि घटना A घटित नहीं हो तो घटना Bघटित नहीं हो सकती है। यदि घटना Aएक बार घटित होती है तो B की घटित होने की प्रायिकता 12है। यदि घटना B के घटित होने की प्रायिकता P को mn के रूप में व्यक्त किया जा सके, तो (m +n) का न्यूनतम मान ज्ञात कीजिये,जहाँ m, n∈ N है।
View Solutionनिम्न फलनों के प्रान्त व परिसर ज्ञात कीजिये।
y=log√5(√2(sinx−cosx)+3)
View Solutionx=2 और x=3, समीकरण 3x^2-x-10 =0 के एक-दूसरे मूल है
View Solutionयदि x2+ax+b=0 एवं x2+a'x+b'=0का एक मूल उभयनिष्ठ हो तो इसका मान है
View Solutionमाना की α,β समीकरण px2+qx+r=0,p≠0 के मूल है | यदि p,q,r समान्तर श्रेणी में हों तथा 1α+1β=4 तो | α−β | का मात्र है :
View Solutionयदि समीकरण x2+px+q=0 के मूल, α,β है और समीकरण x2−rx+s=0 के मूल α4,β4 है, तो समीकरण x2−4qx+2q2−r=0 के सदैव
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solutionमाना p,q∈R, यदि 2−√3 द्विघाती समीकरण x2+px+q=0 का एक मूल है, तो
View Solutionदिया है की समीकरण z2+(p+iq)z+r+is=0 जहाँ p,q,r शून्येतर है के मूल वास्तविक है तब
View Solutionयदि समीकरण x3−3x+2=0 के दो मूल बराबर हो, तो मूल होंगे।
View Solutionयदि a,b विषम पूर्णांक है, तो समीकरण 2ax2+(2a+b)x+b=0,a≠0 के मूल होगा।
View Solutionयदि a,b,c∈Q तो समीकरण (b+c−2a)x2+(c+a−2b)x+(a+b−2c)=0 के मूल है
View Solutionयदि α,β समीकरण x2−3x+1=0 के मूल, हो तो वह समीकरण जिसके 1α−2,1β−2 मूल है, होगी।
View Solution
