In box X there are 4 red and 6 white balls and in box Y there are 3 red and 7 white balls. Now one ball is selected from box X and placed into box Y. Then from box Y one ball is drawn at random.
Then ....... is the probability that selected ball is of red colour and ball placed in box Y from box X is of white colour.Solution in Gujrati
655
755
855
955
The correct Answer is:D
Step by step video, text & image solution for In box X there are 4 red and 6 white balls and in box Y there are 3 red and 7 white balls. Now one ball is selected from box X and placed into box Y. Then from box Y one ball is drawn at random. Then ....... is the probability that selected ball is of red colour and ball placed in box Y from box X is of white colour. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Practice Paper - 13 (Section - A (Choose the correct option))
6 Videos
- PROBABILITYBOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Practice Paper - 13 (Section - B (Answer the following questions))
4 Videos
- PROBABILITYBOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Solutions of NCERT Exemplar Problems (Fillers)
5 Videos
- MATRICES BOOK - KUMAR PRAKASHANCHAPTER - MATRICES EXERCISE - Practice Paper - 3 (Section - D)
1 Videos
- RELATIONS AND FUNCTIONS BOOK - KUMAR PRAKASHANCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Practice Paper - 1 (Section - D)
2 Videos
Similar Questions
If P(A)=611,P(B)=511 amd P(A∪B)=711, find
(i) P(A∩B) (ii) P(A|B) (iii) P(B|A)
View SolutionA couple has two children,
(i) Find the probability that both children are males, if it is known that at least one of the children is male.
(ii) Find the probability that both children are females, if it is known that the elder child is a female.
View SolutionIf A and B are two events such that P(A∣B)=p,P(A)=p,P(B)=13 and P(A∪B)=59 then p = ……….
View SolutionFor matrix A=⎡⎢⎣11112−32−13⎤⎥⎦ . Prove that , A3−6A2+5A+11I=0. Hence find A−1 using it .
View SolutionLet : f:N→N be defined by f(n)={n+12 if n is oddn2 if n is even for all n∈N .
State whether the function f is bijective . Justify your answer.
View SolutionA box B1 contains 1 white ball, 3 red balls, and 2 black balls. An- other box B2 contains 2 white balls, 3 red balls. A third box B3 contains 3 white balls, 4 red balls, and 5 black balls.
If 2 balls are drawn (without replecement) from a randomly selected box and one of the balls is white and the other ball is red the probability that these 2 balls are drawn from box B2 is
View SolutionBox A contains 2 black and 3 red balls , while box B contains 3 black and 4 red balls . Out of these two boxes one is selected at random and the probability of choosing bos A is double that of box B . If a red ball is drawn from the selected box , then the probability that it has come from box B, is
View SolutionA box B1 contains 1 white ball 3 red balls and 2 black balls. Another box B2 contains 2 white balls, 3 red balls and 4 black balls. A third box B3 contains 3 white balls, 4 red balls and 5 black balls.
If 2 balls are drawn (without replacement) from a randomly selected box and one of the ball is white and the other ball is red the probability that these 2 balls are drawn from box B2 is-
View SolutionA box contains 3 red and 7 white balls. One ball is drawn at random and in it placed a ball of the other colour is placed in the box. Now if one ball is drawn at random from the box then the probability that it is a red ball is
View SolutionBox A contains 2 black and 3 red balls, while box B contains 3 black and 4 red balls . Out of these two boxes one is selected at random, and the proability of choosing box A is double that of box B. if a red ball is drawn from the selected box then the proability that is has come from box B is
View SolutionA box X contains 1 white ball, 3 red balls and 2 black balls. Another box Y contains 2 white balls, 3 red balls and 4 black balls. If one ball is drawn from each of the two boxes, then the probability the balls are of different colours is
View SolutionA box B1 contains 1 white ball, 3 red balls, and 2 black balls. An- other box B2 contains 2 white balls, 3 red balls. A third box B3 contains 3 white balls, 4 red balls, and 5 black balls.
If 2 balls are drawn (without replecement) from a randomly selected box and one of the balls is white and the other ball is red the probability that these 2 balls are drawn from box B2 is
View SolutionNumbers of balls in three boxes are as follows.
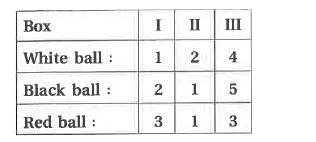
One box is selected of random and two balls are drawn which are of red colour and white colour each.
What is the probability that selected ball is of from box 1 ?
View SolutionIn box one there are 10 white and 3 black balls and in box two there are 3 white and 5 black balls. Two balls are selected at random from box one and placed into box two then one ball is selected at random from box two. Find the probability of an event that selected ball is being white.
View SolutionThere are 2 white and 3 red balls in box A and 4 white, 5 red balls in box B One box is selected at random and one ball is drawn from it. Then ......... is the probability that selected ball is of red colour.
View Solution
