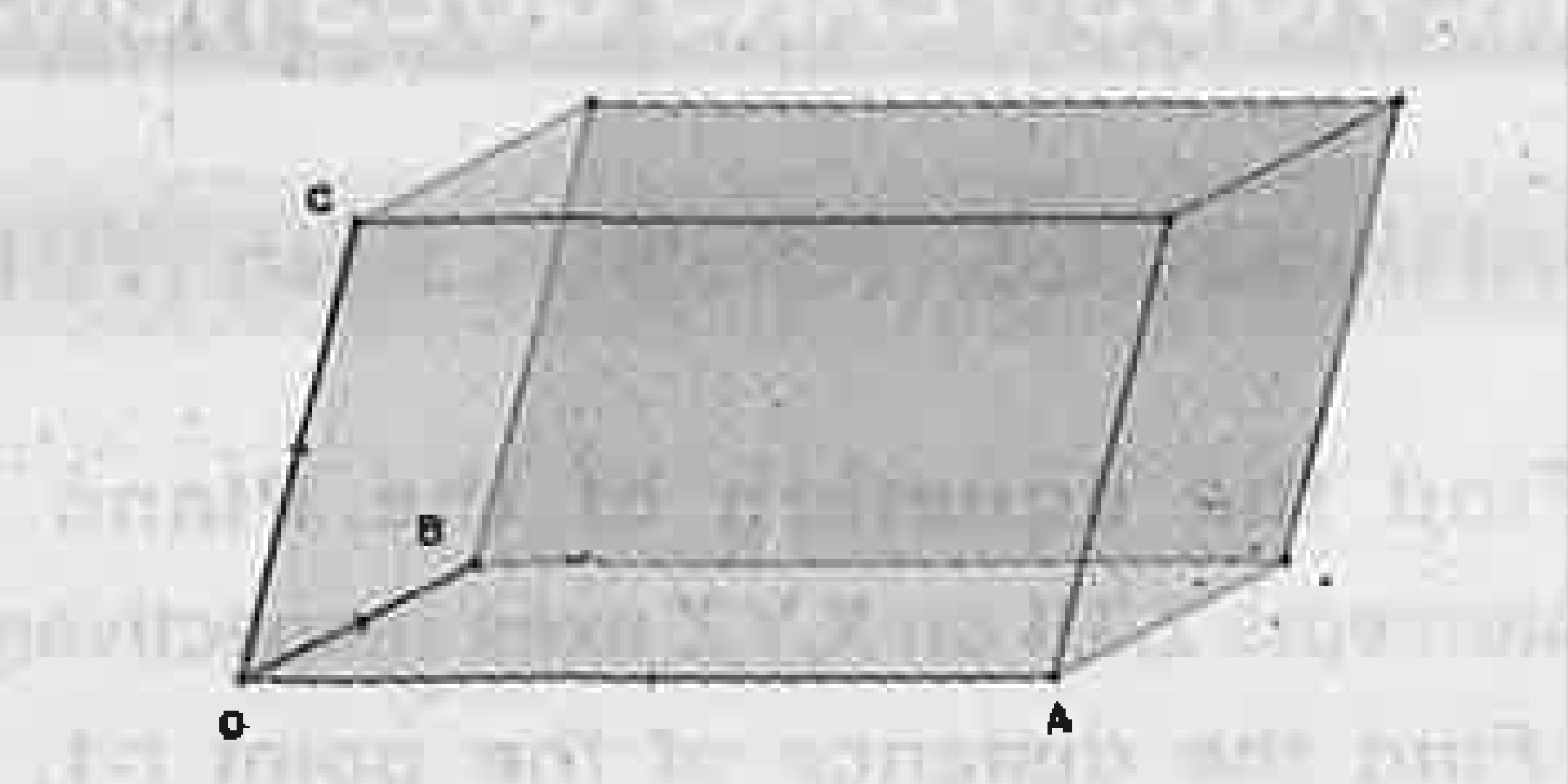
¯¯¯¯¯¯OA=i+2j+3k
¯¯¯¯¯¯OB=i−2j+4k
¯¯¯¯¯¯OC=2i+3j+k
are adjacent sides of the parallelopiped.
Find the base area of the parallelopiped.
(Base determined by ¯¯¯¯¯¯OA and ¯¯¯¯¯¯OB)
 Solution in Malayalam
Solution in Malayalam
Step by step video & image solution for bar(OA)=i+2j+3k bar(OB)=i-2j+4k bar(OC)=2i+3j+k are adjacent sides of the parallelopiped. Find the base area of the parallelopiped. (Base determined by bar(OA) and bar(OB)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Show that the relation R in the set is given by A={x∈Z,0≤x≤12}
R={(a,b):a−b is a multiple of 4} is an equivalence relation.
View SolutionFind →a+→b,→a−→b and →b+→c using the vectors.
→a=3i+4j+k,→b=2i−7j−3k and →c=2i+3j−9k.
View SolutionDeltaABC be an equilateral triangle whose orthocentre is the origin 'O' . If bar (OA)=bar a.bar (OB)=bar b then bar (OC) is
View SolutionDeltaABC be an equilateral triangle whose orthocentre is the origin 'O' . If bar (OA)=bar a.bar (OB)=bar b then bar (OC) is
View SolutionThe orthogonal projection of bar(a)=2i+3j+3k on bar(b)=i-2j+k is
View SolutionOABCD is a pyramid with square base ABCD such that bar(OA),bar(OB),bar(OC),bar(OD) are unit vectors and bar(OA) , bar(OB) = bar(OB) .bar(OC) = bar(OC) . bar(OD) = bar(OD) . bar(OA) =1/2, then volume of the pyramid is
View SolutionVector bar(V) is perpendicular to the plane of vectors bar(a)=2i-3j+k and bar(b)=i-2j+3k and satisfy the condition bar(V)*(i+2j-7k)=10. Find |bar(V)|^(2)
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionThe resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R01_E02_023_Q01.png" width="80%"gt
View SolutionIf diagonals of a parallelogram ABCD intersect each other in M, then ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC+¯¯¯¯¯¯OD =
View Solution¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b,¯¯¯¯¯¯OC=¯c
then volume of the parallelopiped is :
View Solutionयदि ¯¯¯¯¯¯OA=a,¯¯¯¯¯¯OB=−b तथा C,¯¯¯¯¯¯AB पर एक ऐसा बिंदु है की ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है-
View SolutionIf O is the circumcentre, 'H' is the orthocentre of triangle ABC, then show that
¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC=¯¯¯¯¯¯OH
View SolutionΔABC be an equilateral triangle whose orthocentre is the origin 'O'. If ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b then ¯¯¯¯¯¯OC is
View SolutionIf OABC, OCDE, OEFA are adjacent faces of a cube OABCDEF then ¯¯¯¯¯¯OB+¯¯¯¯¯¯OD+¯¯¯¯¯¯OF interms of ¯¯¯¯¯¯OA,¯¯¯¯¯¯OE,¯¯¯¯¯¯OC is
View Solution
