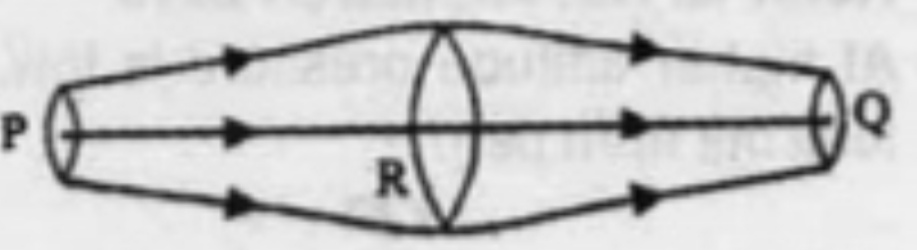
A region of streamline flow of an incompressible fluid shown in the figure. By considering mass conservation in the fluid flow, arrive at the 'equation of continuity'.
 Solution in Malayalam
Solution in Malayalam
Step by step video & image solution for A region of streamline flow of an incompressible fluid shown in the figure. By considering mass conservation in the fluid flow, arrive at the 'equation of continuity'. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Derive F=ma from Newton's law.
View SolutionSolids are least compressible but gases are most compressible. Why?
View SolutionBernouli's equation for a steady streamline flow of a non-viscous incompressible fluid expresses the principle of
View SolutionFor streamline flow of an incompressible fluid, If A is area and v is speed then equation of continuity is
View SolutionObtain an equation of continuity for a flow of fluid on the basis of conservation of mass.
View SolutionState and prove Bernoulli's theorem for a flow of incompressible, non-viscous, and streamlined flow or fluid.
View SolutionState and prove Bernoulli's theorem for a flow of incompressible, non-viscous, and streamlined flow or fluid.
View SolutionWrite the equation of continuity for the flow of incompressible fluids.
View SolutionObtain an equation of continuity for a flow of fluid on the basis of conservation of mass.
View SolutionState and prove Bernoulli's theorem for a flow of incompressible, non-viscous, and streamlined flow or fluid.
View SolutionObtain an equation of continuity for a flow of fluid on the basis of conservation of mass.
View SolutionState and prove Bernoulli's theorem.
View SolutionContinuity equation is law of conservation of volume for incompressible fluid .
View SolutionObtain an equation of continuity for a flow of fluid on the basis of conservation of mass.
View SolutionState and prove Bernoulli's theorem for a flow of incompressible, non-viscous, and streamlined flow or fluid.
View Solution

