z (वास्तविक या काल्पनिक) के उन मानों की संख्या जो कि समीकरणों 1+z+z2+z3+..........+z17=0और 1+z+z2+z3+.......+z13=0 को एक साथ सन्तुष्ट करती है, होगी
1
2
3
4
The correct Answer is:D
Step by step video, text & image solution for z (वास्तविक या काल्पनिक) के उन मानों की संख्या जो कि समीकरणों 1+z+z^2 +z^3+..........+z^17 = 0और 1+z+z^2+z^3+.......+z^13 = 0 को एक साथ सन्तुष्ट करती है, होगी by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERBOOK - BANSAL HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE-1 (SPECIAL DPP-3)
13 Videos
- COMPLEX NUMBERBOOK - BANSAL HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE-1 (SPECIAL DPP-4)
19 Videos
- COMPLEX NUMBERBOOK - BANSAL HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE-5 (RANK BOOSTER)
13 Videos
- BINOMIAL THEOREM BOOK - BANSAL HINDICHAPTER - BINOMIAL THEOREM EXERCISE - EXERCISE - 5 (RANK BOOSTER)
12 Videos
- COMPOUND ANGLE (TRIGONOMETRY PHASE - I) BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE - 5 (RANK BOOSTER)
10 Videos
Similar Questions
चित्र में सम्मिश्र समतल में कुछ संख्याऐं दर्शायी गयी है तथा वृत्त एक इकाई वृत्त है जिसका केन्द्र मूल बिन्दु है, तब निम्न में से कौनसा एक F का प्रतिलोम होगा
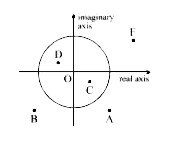
View Solutionयदि z1 व z2 दो अशून्य (non - zero) सम्मिश्र संख्याएँ इस प्रकार है कि |z1+z2|=|z1|+|z2|, तब कोणांक (z1) - कोणांक (z2) का मान होगा
View Solutionदर्शाइये की गुणनफल, [1+(1+i2)][1+(1+i2)2][1+(1+i2)22].......[1+(1+i2)2n] का मान (1−122n)(1+i) के बराबर है, जहाँ n≥2 है।
View Solutionश्रेणी में (1+x)2012+(1+x2)2011+(1+x3)2010 असमान पदों की संख्या ज्ञात कीजिए।
View Solutionमाना cosπ7+cos2π7−2 cos3π7 का यथार्थ मान एक परिमेय संख्या है जो कि pq के रूप में है, जहाँ p तथा q पूर्णांक है | (p + q) का मान ज्ञात कीजिए |
View SolutionNumber of values of z (real or complex) simultaneously satisfying the system of equations 1+z+z2+z3++z17=0 and 1+z+z2+z3++z13=0 is
View SolutionThe number of values of z (real or complex) e simultaneously satisfying the system of equations 1+z+z2+z3+...z17=0and1+z+z2+z3+..+z13=0 is
View SolutionIf ={z:(1+2i)bar(z)+(1-2i)z+2=0) and B={z:(3+2i)+(3-2i)z+3=0, then
View Solutionयदि किसी समबाहु त्रिभुज के शीर्ष z1,z2,z3 हो ताकि |z1|=|z2|=|z3| तो साबित करे z1+z2+z3=0
View Solutionयदि z2+z+1=0, जहाँ z एक सम्मिश्र संख्या है तब
(z+1z)2+(z2+1z2)2+(z3+1z3)2+...+(z6+1z6)2 का मान होगा -
View Solutionसम्मिश्र संख्याओं z कि संख्या जो इस प्रकार |z−1|=|z+1|=|z−i|है, है :
View Solutionयदि z2+z+1=0 जहाँ z एक सम्मिश्र संख्या है, तो (z+1z)2+(z2+1z2)2+(z3+1z3)2+......(z6+1z6)2 का मान है -
View SolutionIf z^(2)+z+1=0 , where z is a complex number, then the value of (z+(1)/(z))^(2)+(z^(2)+(1)/(z^(2)))^(2)+(z^(3)+(1)/(z^(3)))^(2)+....+(z^(6)+(1)/(z^(6)))^(2) is
View SolutionIf z^(2)+z+1=0 , where z is a complex number, then the value of (z+(1)/(z))^(2)+(z^(2)+(1)/(z^2))^(2)+(z^(3)+(1)/(z^3))^(2)+"……"+(z^(6)+(1)/(z^6))^(2) is
View SolutionX(वास्तविक या सम्मिश्र) के मानों की संख्या जो समीकरण निकाय 1+z+z2+z3+……….+z17=0 तथा 1+z+z2+z3+…………+z13=0 को एक साथ संतुष्ट करते है होगी:
View Solution
