श्रेणी S=sin206∘+sin208∘+sin210∘+....+sin1234∘ का योगफल है : (i) 515 (ii) cosec(1)∘ (iii) 0 (iv) 12
515
cosec(1)∘
0
12
The correct Answer is:C
Step by step video, text & image solution for श्रेणी S = sin 206^(@) + sin 208^(@) + sin 210^(@) + ....+sin 1234^(@) का योगफल है : (i) 515 (ii) "cosec" (1)^(@) (iii) 0 (iv) (1)/(2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPOUND ANGLE (TRIGONOMETRY PHASE - I) BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE - 2
20 Videos
- COMPOUND ANGLE (TRIGONOMETRY PHASE - I) BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE -3 SECTION-A (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS)
9 Videos
- COMPOUND ANGLE (TRIGONOMETRY PHASE - I) BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE -1 SPECIAL DPP-5
10 Videos
- COMPLEX NUMBERBOOK - BANSAL HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE-5 (RANK BOOSTER)
13 Videos
- CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)BOOK - BANSAL HINDICHAPTER - CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)EXERCISE - EXERCISE - 5
18 Videos
Similar Questions
यदि X=sin(θ+7π12)+sin(θ−π12)+sin(θ+3π12),Y=cos(θ+7π12)+cos(θ−π12)+cos(θ+3π12) हो, तो सिद्ध कीजिए कि XY−YX=2tan2θ.
View Solutionइकाई त्रिज्या के तीन सिक्के (coins) एक समबाहु त्रिभुज में इस प्रकार से रखे जाते है कि वे परस्पर एक दूसरे को तथा त्रिभुज की भुजाओं को स्पर्श करते है तो त्रिभुज का क्षेत्रफल होगा
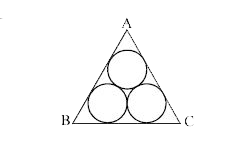
View Solutionयदि व्यंजक 15sec2θ−tan2θ+4 cosec2θ का अधिकतम मान pq है, (जहाँ p तथा q सह अभाज्य है) तब (p + q) का मान है : (i) 14 (ii) 15 (iii) 16 (iv) 18
View Solutionदर्शाइये की गुणनफल, [1+(1+i2)][1+(1+i2)2][1+(1+i2)22].......[1+(1+i2)2n] का मान (1−122n)(1+i) के बराबर है, जहाँ n≥2 है।
View Solutionबिन्दु P(h, k) से परवलय x2=8y पर तीन अभिलम्ब डाले गये है तथा m1,m2 तथा m3 इन तीनों की प्रवणताऐं है। इन तीनों अभिलम्बों की प्रवणताओं का बीजगणितीय योग ज्ञात कीजिए।
View SolutionProve the following identities: (sinA+secA)2+(cosA+c o s e cA)2=(1+secAcosecA)2 cot2A(secA−11+sinA)+sec2A(sinA−11+secA)=0
View SolutionEvaluate each of the following:
(i)sin(cot−1(43))
(ii) sin(sec−1(1715))
(iii) sin(c o s e c−1178)
View Solutionsin^(2) 50^(@)+cos^(2) 130^(@) = (i) 0 (ii) 1 (iii) -1 (iv) -2
View Solution(cot^(2)A)/((cosec A+1)^(2))=(1-sin A)/(1+sin A)
View SolutionFind the principal values of the following
(i) sin−1(sin1)
(ii) sin−1(sin2)
(iii) sin−1(sin10)
(iv) sin−1(sin20)
(v) sin−1(sin100)
(vi) sin−1(sin.29π5)
View SolutionWithout using trigonometric tables, prove that :
(i)sin43∘cos47∘+cos43∘sin47∘=1
(ii)cos38∘cos52∘−sin52∘=0
(iii)sec50∘sin40∘+cos40∘cosec50∘=2
(iv)sec70∘sin20∘−cos20∘−cosec70∘=0
View SolutionProve that
(i)tanA+sinAtanA−sinA=secA+1secA−1
(ii)cotA−cosAcotA+cosA=cosecA−1cosecA+1
View Solutionहल करें
(i) cosθ=12 (ii)sinθ=−1
(iii) 3tan2θ=1 (iv)2sinθ=√3
(iv) sin=x−√32
View SolutionFind the principal values of the following
(i) sin−1(sin1) (ii) sin−1(sin2)
(iii) sin−1(sin10)
View SolutionProve that: (i) cos55∘sin35∘+sin55∘cos35∘=1
(ii) tan72∘cot18∘−cot72∘tan18∘=0
(iii) sec70∘sin20∘+cosec70∘cos20∘=2
View Solution
