The following questions consist of two statements, one labelled as 'Statement I' and the other 'Statement II'. You have to examine these two statements carefully and decide if the Statement I and the Statement II, are individually true and if so, whether the Statement II is the correct explanation for the given Statement I. Select your answer to these items using the codes given below and then select the correct option.
Statement-1 : sin−1(1√e)>tan−1(1√π)
Statement-2 : sin−1x>tan−1y for x>y,∀x,y∈(0,1)Solution in Telugu
Both I and II are individually trueand II is the correct explanation of I
Both I and II are individually true but II is not the correct explanation of I
I is true but II is false
I is false but II is true
The correct Answer is:A
Step by step video, text & image solution for The following questions consist of two statements, one labelled as 'Statement I' and the other 'Statement II'. You have to examine these two statements carefully and decide if the Statement I and the Statement II, are individually true and if so, whether the Statement II is the correct explanation for the given Statement I. Select your answer to these items using the codes given below and then select the correct option. Statement-1 : sin^(-1)(1/sqrt(e)) gt tan^(-1)(1/sqrt(pi)) Statement-2 : sin^(-1)x gt tan^(-1)y" for "x gt y, forallx, y in (0,1) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INVERSET TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSET TRIGONOMETRIC FUNCTIONSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET (ADVANCED) MATRIX MATCHING TYPE QUESTIOS)
1 Videos
- INVERSET TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSET TRIGONOMETRIC FUNCTIONSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET (ADVANCED) INTEGER ANSWER TYPE QUESTIOS)
1 Videos
- INVERSET TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSET TRIGONOMETRIC FUNCTIONSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIOS)
3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - PRACTICE EXERCISE
37 Videos
- LIMITSBOOK - AAKASH SERIESCHAPTER - LIMITSEXERCISE - PRACTICE EXERCISE
143 Videos
Similar Questions
Match the items of Column I with the items Column II
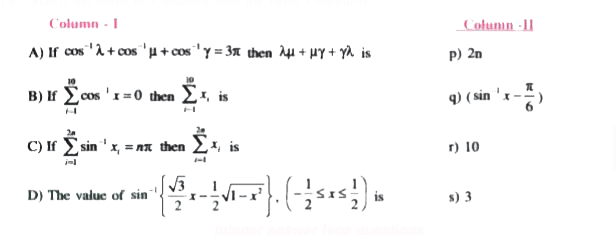
View SolutionThe solution set of inequality (cot−1x)(tan−1x)+(2−π2)cot−1x−3tan−1x−3(2−π2)>0 is (a, b) then the value of cot−1a+cot−1b is
View SolutionWhile defining inverse trigonometric functions, a new system is followed where domains and ranges have been redefined as follows:
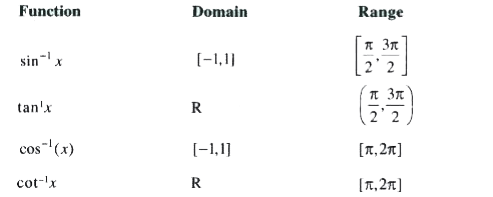
sin−1(−x) is equal to
View SolutionThe value of cot−1(cot(5π6))=
View SolutionLtx→0x2−5x+72x2+3x−1=
View SolutionDirection : These questions have statement I and statement II. of the four choice given below , choose the one that best describes the two statements.
A: Statement I is true, statement II is true , statement II is a correct explanation for statement I.
B : Statement I is true statement II is true , statement II is not a correct explanation for statement I.
C : statement I is true ,statement II is false.
D: Statement I is false, statement II is true.
Statement I : The resolving power of a telescope is more if the diameter of the objective lens is more.
Statement II: Objective lens of large diameter collects more light.
View Solutionनिम्न प्रश्नों में दो कथन दिए गए है, एक को कथन - I तथा दूसरे को कथन - II के रूप में अंकित किया गया है।
(A) कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
(B) कथन- सत्य है, कथन-II सत्य है , कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
(C) कथन - I सत्य है परन्तु कथन - II असत्य है।
(D) कथन - I असत्य है परन्तु कथन - II सत्य है।
कथन-I: द्विघात समीकरण 10x2−28x+17=0 का कम से कम एक मूल [1,2] में होगा।
क्योंकि
कथन-II: f(x)=e10x(x−1)(x−2),[1,2] में रोल प्रमेय के सभी प्रतिबन्धों को सन्तुष्ट करता है।
View Solutionनिम्न प्रश्नों में दो कथन दिए गए है, एक को कथन - I तथा दूसरे को कथन - II के रूप में अंकित किया गया है।
(A) कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
(B) कथन- सत्य है, कथन-II सत्य है , कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
(C) कथन - I सत्य है परन्तु कथन - II असत्य है।
(D) कथन - I असत्य है परन्तु कथन - II सत्य है।
माना f:R→R,f(x)=x3+x2+3x+sinx है।
कथन-I: f(x) एकैकी होगा।
क्योंकि
कथन-II: f(x) ओसमान फलन है।
View SolutionThe following questions consist of two statements, one labelled as 'Statement I' and the other 'Statement II'. You have to examine these two statements carefully and decide if the Statement I and the Statement II, are individually true and if so, whether the Statement II is the correct explanation for the given Statement I. Select your answer to these items using the codes given below and then select the correct option.
Statement-1 : cosec−1(12+1√2)>sec−1(12+1√2)
Statement-2 : cosec−1x<sec−1x if 1≤x<√2
View SolutionThe following questions consist of two statements, one labelled as 'Statement I' and the other 'Statement II'. You have to examine these two statements carefully and decide if the Statement I and the Statement II, are individually true and if so, whether the Statement II is the correct explanation for the given Statement I. Select your answer to these items using the codes given below and then select the correct option.
Statement-1 : The value of tan−12+tan−13=3π4
Statement-2 : If x>0,y>0,xy>1 then tan−1x+tan−1y=π+tan−1(x+y1−xy)
View SolutionThe following questions consist of two statements, one labelled as 'Statement I' and the other 'Statement II'. You have to examine these two statements carefully and decide if the Statement I and the Statement II, are individually true and if so, whether the Statement II is the correct explanation for the given Statement I. Select your answer to these items using the codes given below and then select the correct option.
Statement-1 : sin−1(1√e)>tan−1(1√π)
Statement-2 : sin−1x>tan−1y for x>y,∀x,y∈(0,1)
View SolutionThe following questions consist of two statements, one labelled as 'Statement I' and the other 'Statement II'. You have to examine these two statements carefully and decide if the Statement I and the Statement II, are individually true and if so, whether the Statement II is the correct explanation for the given Statement I. Select your answer to these items using the codes given below and then select the correct option.
Statement 1 : sin−1(sin5)>x2−4x has many solutions lying in the interval (2−√9−2π,2+√9−2π)
Statement 2 : Sin−1(Sin5)=5−2π
View SolutionThe following questions consist of two statements, one labelled as 'Statement I' and the other 'Statement II'. You have to examine these two statements carefully and decide if the Statement I and the Statement II, are individually true and if so, whether the Statement II is the correct explanation for the given Statement I. Select your answer to these items using the codes given below and then select the correct option.
Statement - 1 : Let |x|≤1, then the value of sin−1[cos(sin−1x)]+cos−1[sin(cos−1x)] is π/2
Statement - 2 : For the values of x∈[−1,1]cos(sin−1x)=sincos−1x
View SolutionThe following questions consist of two statements, one labelled as 'Statement I' and the other 'Statement II'. You have to examine these two statements carefully and decide if the Statement I and the Statement II, are individually true and if so, whether the Statement II is the correct explanation for the given Statement I. Select your answer to these items using the codes given below and then select the correct option.
Statement - 1 : If a+b=0,a≠0 then sin−1ax+cos−1bx=3π2 has no solution
Statement - 2 : sin−1x+cos−1x=π2,−1≤x≤1
View SolutionThis question has statement I and Statement II. Of the four choices given after the statements, choose the one that best describes the two Statements.
(1) Statement-I is true, Statement-II is true, Statement-II is a correct explanation of Statement-I
(2) Statement-I is true, Statement-II is true,Statement-II is not a correct explanation of Statement-I
(3)Statement-I is a true , Statement-II is false
(4) Statement-I is false, Statement-II is true
Statement-I: The dipole moment helps to predict whether a molecule is polar or non-polar
Statement-II: The dipole moment helps to predict the geometry of molecules.
View SolutionThis question has statement-I and statement-II of the four choices given after the statement.Choose the one that best describes the two statements
Statement-I is true Statement-II is true Statement-II is a correct explanation of statement-I
Statement-I is true Statement-II is true Statement-II is not a correct explanation of statement-I
Statement--I is true , Statement-II is false
Statement-I is false statement-II is true
Both statement-I and statement-II are false
Statement - I : If a body moving along a circular path has a constant speed, then there is no force acting on it.
Statement- II : The direction of velocity of the body moving in a circular path is not changing.
View Solution
