If sin−1(cos−1x)<1 and cos−1(cos−1x)<1 then x in Solution in Telugu
(Sin1,Sin(sin1))
(cos(cos1),cos(sin1))
(cos(sin1),cos(cos1))
ϕ (empty set)
The correct Answer is:C
Step by step video, text & image solution for If sin^(-1)(cos^(-1)x)lt1 and cos^(-1)(cos^(-1)x)lt1 then x in by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INVERSET TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSET TRIGONOMETRIC FUNCTIONSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
6 Videos
- INVERSET TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSET TRIGONOMETRIC FUNCTIONSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIOS)
3 Videos
- INVERSET TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSET TRIGONOMETRIC FUNCTIONSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-I (MAIN) SINGLE ANSWER TYPE QUESTIONS)
25 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - PRACTICE EXERCISE
37 Videos
- LIMITSBOOK - AAKASH SERIESCHAPTER - LIMITSEXERCISE - PRACTICE EXERCISE
143 Videos
Similar Questions
Which of the following is/are true
View SolutionWhile defining inverse trigonometric functions, a new system is followed where domains and ranges have been redefined as follows:
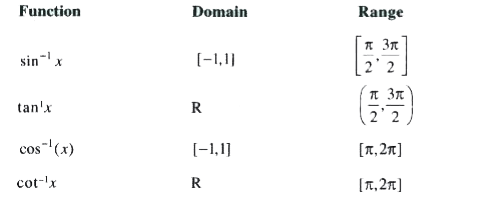
sin−1(−x) is equal to
View SolutionCos−1(41/49)Sin−1(2/7)=
View SolutionThe value of cot−1(cot(5π6))=
View SolutionLtx→0x2−5x+72x2+3x−1=
View Solutiony=cos−1(2x1+x2),−1<x<1
View SolutionIf |a|lt1| b|lt1and|x|lt1 then the solution of sin^(-1)((2a)/(1+a^(2)))-cos^(-1)((1-b^(2))/(1+b^(2)))=tan^(-1)((2x)/(1-x^(2))) is
View Solutionsin(tan−1x),|x|<1 बराबर होता है:
View Solutioncos−11−x21+x2,|x|<1
View SolutionDifferentiate the following w.r.t.x. ecos−1(√1−x2),|x|<1
View Solutionयदि |x|<1,तो sin(tan−1x)=
View SolutionFind dydx in the following :
y=cos−1(2x1+x2),−1<x<1.
View SolutionFind dydx in the following :
y=cos−1(2x1+x2),−1<x<1.
View SolutionFind dydx in the following :
y=cos−1(2x1+x2),−1<x<1.
View Solutionsin(tan−1x),|x|<1 is equal to
View Solution
