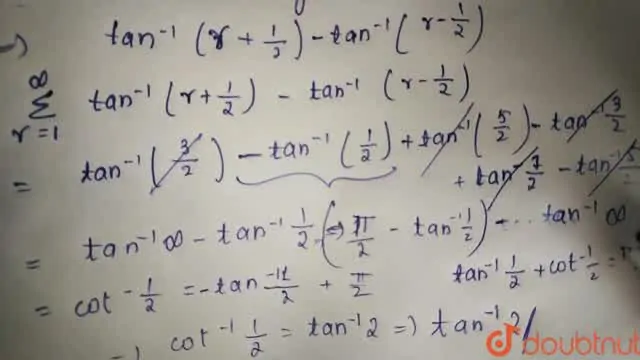Sum of infinite terms of the series ${cot}^{- 1} (1^{2} + \frac{3}{4}) + {cot}^{- 1} (2^{2} + \frac{3}{4}) + {cot}^{- 1} (3^{2} + \frac{3}{4}) + \dots . .$ is Solution in Telugu

$\frac{π}{4}$

${tan}^{- 1} 2$

${tan}^{- 1} 3$

${tan}^{- 1} 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for Sum of infinite terms of the series cot^(-1)(1^(2)+3/4)+cot^(-1)(2^(2)+3/4)+cot^(-1)(3^(2)+3/4)+….. is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS INVERSE TRIGNOMETRIC FUNCTIONS

Topper's Solved these Questions

BOOK - AAKASH SERIESCHAPTER - INVERSE TRIGNOMETRIC FUNCTIONSEXERCISE - LECTURE SHEET (EXERCISE - II) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
4videos
INVERSE TRIGNOMETRIC FUNCTIONS
BOOK - AAKASH SERIESCHAPTER - INVERSE TRIGNOMETRIC FUNCTIONSEXERCISE - LECTURE SHEET (EXERCISE - II) (MATRIX MATCHING TYPE QUESTIONS)
1videos
INVERSE TRIGNOMETRIC FUNCTIONS
BOOK - AAKASH SERIESCHAPTER - INVERSE TRIGNOMETRIC FUNCTIONSEXERCISE - LECTURE SHEET (EXERCISE - I DOMAIN, RANGE, PRINCIPAL VALUES, BASIC PROPERTIES) (INTEGER TYPE QUESTIONS)
5videos
INVERSE TRIGNOMETRIC FUNCTIONS
BOOK - AAKASH SERIESCHAPTER - HYPERBOLIC FUNCTIONS EXERCISE - PRACTICE SHEET EXERCISE-II (STRAIGHT OBJECTIVE TYPE QUESTIONS)
18videos
HYPERBOLIC FUNCTIONS
BOOK - AAKASH SERIESCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - PRACTICE EXERCISE
37videos
INVERSE TRIGONOMETRIC FUNCTIONS

Similar Questions

If $A = 2 {tan}^{- 1} (2 \sqrt{2} - 1) and B = 3 {sin}^{- 1} (1 / 3) + {sin}^{- 1} (3 / 5)$ then
06:39
View Solution
Let (x, y) be such that ${sin}^{- 1} (a x) + {cos}^{- 1} (y) + {cos}^{- 1} (b x y) = π / 2$ . Match the statements in column I with statements in column II.
$\begin{matrix} Column I & Column II A) If a = 1 and b = 0, then (x, y) & p) lies on the circle x^{2} + y^{2} = 1 B) If a = 1 and b = 1, then (x, y) & q) lies on (x^{2} - 1) (y^{2} - 1) = 0 C) If a = 1 and b = 2, then (x, y) & r) lies on y = x D) If a = 2 and b = 2, then (x, y) & s) lies on (4 x^{2} - 1) (y^{2} - 1) = 0 \end{matrix}$
02:52
View Solution
If the domain of the function $f (x) = \sqrt{3 {cos}^{- 1} (4 x) - π}$ is [a,b], then the value of (4a+64b) is
04:29
View Solution
The domain of ${cos h}^{- 1} (2 x)$ is
03:11
View Solution
The value of ${cot}^{- 1} (cot (\frac{5 π}{6})) =$
05:31
View Solution
The sum of the infinite series ${cot}^{- 1} (\frac{7}{4}) + {cot}^{- 1} (\frac{19}{4}) + {cot}^{- 1} (\frac{39}{4}) ... . \infty$
03:46
View Solution
If the sum of first 16 terms of the series $s = {cot}^{- 1} (2^{2} + \frac{1}{2}) + {cot}^{- 1} (2^{3} + \frac{1}{2^{2}}) + {cot}^{- 1} (2^{4} + \frac{1}{2^{3}}) +$ up to terms is ${cot}^{- 1} (\frac{1 + 2^{n}}{2 (2^{16} - 1)})$ , then find the value of $n .$
05:31
View Solution
The value of 2(cot^(-1))(1)/(2)-(cot^(-1))(4)/(3) is
04:12
View Solution
The sum to infinite terms of the series cot^(-1)(2^(2)+(1)/(2))+cot^(-1)(2^(3)+(1)/(2^(2)))+cot^(-1)(2^(4)+(1)/(2^(3)))+
03:22
View Solution
The sum of the infinite terms of the series ${cot}^{- 1} (1^{2} + \frac{3}{4}) + {cot}^{- 1} (2^{2} + \frac{3}{4}) + {cot}^{- 1} (3^{2} + \frac{3}{4}) + ... + \infty$ is equal to a. ${tan}^{- 1} (1)$ b. ${tan}^{- 1} (2)$ c. ${tan}^{- 1} 2$ d. $\frac{3 π}{4} - {tan}^{- 1} 3$
02:46
View Solution
Sum to infinite terms the series: ${cot}^{- 1} (1^{2} + \frac{3}{4}) + {cot}^{- 1} (2^{2} + \frac{3}{4}) + {cot}^{- 1} (3^{2} + \frac{3}{4}) + \dots .$
03:35
View Solution
Sum of infinite terms of the series ${cot}^{- 1} (1^{2} + \frac{3}{4}) + {cot}^{- 1} (2^{2} + \frac{3}{4}) + {cot}^{- 1} (3^{2} + \frac{3}{4}) +$ ... is
06:51
View Solution
Find the sum to n terms of the series $S_{n} = {cot}^{- 1} (2^{2} + \frac{1}{2}) + {cot}^{- 1} (2^{3} + \frac{1}{2^{2}}) + {cot}^{- 1} (2^{4} + \frac{1}{2^{3}}) + ... . .$ upto n terms ?
06:52
View Solution
Value of $2 {cot}^{- 1} \frac{1}{2} - {cot}^{- 1} \frac{4}{3}$ is-
09:25
View Solution
$2 {cot}^{- 1} . \frac{1}{2} - {cot}^{- 1} . \frac{4}{3}$ का मान है -
11:12
View Solution

AAKASH SERIES-INVERSE TRIGNOMETRIC FUNCTIONS-LECTURE SHEET (EXERCISE - II) (STRAIGHT OBJECTIVE TYPE QUESTIONS)

If we consider only the principle values of the inverse trigonometric ...
08:50
Find the value of tan(2"Tan"^(-1)(1/5)-(pi)/4)
03:08
If x,y,z are in A.P and Tan^(-1) x, Tan^(-1) y and Tan^(-1) z are als...
04:15
Cot^(-1)(sqrt(Cos alpha))-Tan^(-1)( sqrt(Cos alpha))=x then Sinx=
04:29
The number of solutions of the equation Tan^(-1)(x-1)+Tan^(-1)(x+1)=Ta...
02:10
The value of tan[Tan^(-1)(1/(a+b))+Tan^(-1)(b/(a^(2)+ab+1))] is
04:01
The arithmetic mean of the non-zero solutions of the equation "Tan"^...
06:35
If a,b,c, are positive then tan^(-1)sqrt((a(a+b+c))/(bc))+tan^(-1)sq...
05:06
If alpha, beta, gamma are the roots of the equation x^(3)+mx^(2)+3x+m=...
06:36
If Cos^(-1)x-Cos^(-1)(y/2)=alpha" then "4x^(2)-4xycosalpha+y^(2)=
04:15
If sin^(-1)x+sin^(-1)y+sin^(-1)z=(3pi)/z then the value of sum((x^(201...
02:11
If Cos^(-1)x+Cos^(-1)y+Cos^(-1)z=pi,"then "x^(2)+y^(2)+z^(2)+2xyz=
03:28
The value of alpha such that sin^(-1)""2/sqrt(5), sin^(-1)""3/sqrt(10)...
Text Solution
sum(r=1)^(n)sin^(-1)((sqrt(r)-sqrt(r-1))/sqrt(r(r+1))) is equal to
03:44
sum(m=1)^(oo)Tan^(-1) ((2m)/(m^(4)+m^(2)+2))=
04:50
The value of "tan"^(-1)4/7+"tan"^(-1)4/19+"tan"^(-1)4/39+"tan"^(-1)4/6...
04:56
The sum of series sec^(-1)sqrt(2)+"sec"^(-1)(sqrt(10))/3+"sec"^(-1)(sq...
04:17
Sum of infinite terms of the series cot^(-1)(1^(2)+3/4)+cot^(-1)(2^(2)...
07:11
Tan^(-1)(1/3)+Tan^(-1)(2/9)+Tan^(-1)(4/33)+…… infty
05:28
The value of cot(sum(n=1)^(23)cot^(-1)(1+sum(k=1)^(n)2k)) is
06:47

Home
Ask Doubt
Profile

Sum of infinite terms of the series cot−1(12+34)+cot−1(22+34)+cot−1(32+34)+….. is Solution in Telugu

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

AAKASH SERIES-INVERSE TRIGNOMETRIC FUNCTIONS-LECTURE SHEET (EXERCISE - II) (STRAIGHT OBJECTIVE TYPE QUESTIONS)

Sum of infinite terms of the series ${cot}^{- 1} (1^{2} + \frac{3}{4}) + {cot}^{- 1} (2^{2} + \frac{3}{4}) + {cot}^{- 1} (3^{2} + \frac{3}{4}) + \dots . .$ is Solution in Telugu