[Telugu] A line OA length r starts from its initial position OX and tr

${tan 9}^{\circ} - {tan 27}^{\circ} - {tan 63}^{\circ} + {tan 81}^{\circ}$ =

01:31

View Solution

If $4 {sin 27}^{\circ} = \sqrt{α} + \sqrt{β}$ then the sum of the digits in ${(α + β + α β + 2)}^{4}$

02:31

View Solution

If $(x - a) cos θ + y sin θ = (x - a) cos ϕ + y sin ϕ = a and tan (ϕ / 2) = 2 b$ then

02:12

View Solution

Given f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )

04:21

View Solution

$(\frac{sin A}{1 - cos A}) - (\frac{1 - cos A}{sin A}) =$

06:56

View Solution

If sin alpha=(1)/(2) and cos theta=(1)/(3) then the values of alpha+theta( if theta,alpha are both acute angles) will lie in the interval

07:04

View Solution

sin(3 theta+alpha)+sin(3 theta-alpha)+sin(alpha-theta)-sin(alpha+theta)=cos alpha

View Solution

A line OA of length r starts from its initial position OX and traces an angle AOB = $α$ in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = $3 θ$ ( where $α > 3 θ$ ). L is the foot of the perpendicular from C on OA. Also, $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{1 - r cos α}{r sin α}$ is equal to

05:52

View Solution

A line OA of length r starts from its initial position OX and traces an angle AOB = $α$ in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = $3 θ$ ( where $α > 3 θ$ ). L is the foot of the perpendicular from C on OA. Also, $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{2 r sin α}{1 + 2 r cos α}$ is equal to

03:57

View Solution

A line OA of length r starts from its initial position OX and traces an angle AOB = $α$ in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = $3 θ$ ( where $α > 3 θ$ ). L is the foot of the perpendicular from C on OA. Also, $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{2 r^{2} - 1}{r}$ is equal to

13:05

View Solution

If $cos (θ - α), cos (θ), Cos (θ + α)$ are in H.P. and $cos α \neq 1$ , then angle $α$ lie in the

View Solution

Let $O P = r and ∠ X O P = θ$ then the position of P in polar coordinate system is represented by $(r, θ)$ OX and O are called the initial line and pole respectively.
If p be the length of perpendicular from origin to line and if $α$ is the angle which the perpendicular to the line makes with the initial line . The equation of line is given by r cos $(θ - α) = p$
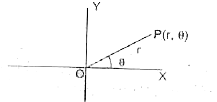
ocr_image
Perpendicular distance from pole to the line $\frac{l}{r} = 4 cos θ + 2 sin θ$ is

View Solution

A line OA of length r starts from its initial position OX and traces an angle AOB = $α$ in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = $3 θ$ ( where $α > 3 θ$ ). L is the foot of the perpendicular from C on OA. Also, $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{2 r sin α}{1 + 2 r cos α}$ is equal to

View Solution

A line OA of length r starts from its initial position OX and traces an angle AOB = $α$ in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = $3 θ$ ( where $α > 3 θ$ ). L is the foot of the perpendicular from C on OA. Also, $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{2 r^{2} - 1}{r}$ is equal to

View Solution

A line OA length r starts from its initial position OX and traces an angle $A O B = α$ in the anticlockwise direction. It then traces back in the clockwise direction an angle $B O C = 3 θ$ ( where $α > 3 θ$ ) . L is the foot of the the perpendicular from C on OA. $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{1 - r cos α}{r sin α}$ is equal to

View Solution

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

AAKASH SERIES-MULTIPLE & SUBMULTIPLE -LECTURE SHEET (EXERCISE - I) (Linked Comprehension Type Questions)