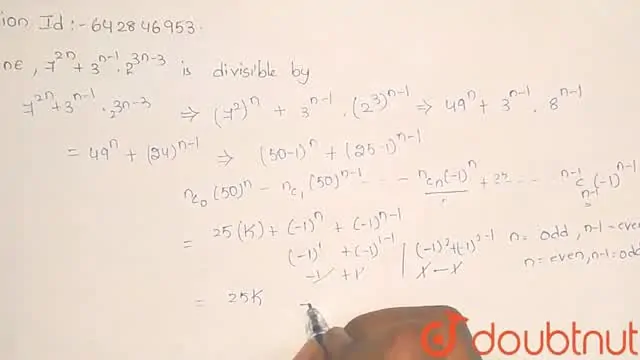
∀n∈,72n+3n−1.23n−3 is divisible bySolution in Telugu
50
25
2425
2550
The correct Answer is:B
Step by step video, text & image solution for AA n in , 7^(2n) + 3^(n-1) . 2^(3n-3) is divisible by by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - AAKASH SERIESCHAPTER - MATHEMATICAL INDUCTIONEXERCISE - PRACTICE SHEET (EXERCISE-I) LEVEL-I (Principle of Mathematical Induction) (Straight Objective Type Questions)55videos
MATHEMATICAL INDUCTION
- BOOK - AAKASH SERIESCHAPTER - LOCUSEXERCISE - PRACTICE EXERCISE37videos
LOCUS
- BOOK - AAKASH SERIESCHAPTER - MATRICES EXERCISE - LINEAR EQUATIONS - PRACTICE EXERCISE15videos
MATRICES
Similar Questions
Let P(n) denote the statement that n2+n is odd. It is seen that P(n)⇒P(n+1),P(n) is true for all
03:39View SolutionThe locus of the point which is equidistant to the coordinate axes is
05:24View SolutionThe solution of 7x+5y−13z+4=0,9x+2y+11z=37,3x−y+z=2 is
06:31View Solution7^(2n)+2^(3n-3)*3^(n-1) is divisible by 25
03:31View Solution7^(2n)+2^(3n-3).3^(n-1) is divisible by 25
08:17View SolutionProve the following by the principle of mathematical induction: 72n+23n−3.3n−1 is divisible 25 for all n∈N.
01:52View Solutionसिद्ध किजिये कि 72n+23n−3।3n−1 प्रत्येक प्राकृतिक संख्या n के लिये 25 से विभाज्य है ।
06:13View Solution72n+23n−3.3n−1, प्रत्येक प्राकृतिक संख्या n के लिये किस से विभाज्य है।
View SolutionIn n∈N, then (32n+2−23n−9) is always divisible by -
02:07View SolutionFor every natural number n, show that 72n+23n−3⋅3n−1 is always divisible by 25.
07:49View SolutionIf n is a positive integer, then 2.42n+1+33n+1 is divisible by :
05:06View SolutionIf n is a positive integer, then 2.42n+1+33n+1 is divisible by :
07:34View SolutionA) 49n+16n+1 is divisible by A(n∈N)
B) 32n+7 is divisible by B(n∈N)
C) 4n−3n−1 is divisible by C(n∈n)
D) 33n−26n−1 is divisible by D(n∈N)
then the increasing order of A, B, C, D is05:43View SolutionProve that ∀n∈N
33n−26n−1 is divisible by 676.05:01View Solution72n+23n−33n−1 is divisible by 25 for any natural number n>1.
02:44View Solution