P is the centre of mass of a system of four point masses A,B,C and D, which are coplanar but not collinear.
(a) P may or may not coincide with one of the point masses
(b) P must lie within or on the edge of atleast one of the triangles formed by taking A,B, C and D three at a time
(c ) P must lie on a line joining two of the points A,B,C,D
(d ) P lies out side the quadrangle ABCDSolution in Telugu
a & b are correct
c & d are correct
a & c are correct
b & d are correct
The correct Answer is:A
Step by step video, text & image solution for P is the centre of mass of a system of four point masses A,B,C and D, which are coplanar but not collinear. (a) P may or may not coincide with one of the point masses (b) P must lie within or on the edge of atleast one of the triangles formed by taking A,B, C and D three at a time (c ) P must lie on a line joining two of the points A,B,C,D (d ) P lies out side the quadrangle ABCD by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-II
109 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE
99 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Problems
103 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
Similar Questions
Centre of mass of two particle with masses 2 kg and 1 kg locsted at (1, 0, 1) and (2, 2, 0) has the co - ordinates of
View SolutionThe centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
View SolutionIf the distance between the centres of the atoms of potassium and bromine in KBr (potassium - bromide) molecule is 0.282×10−9m, find the centre of mass of this particle system from potassium (mass of bromine = 80 u, and of potassium = 39 u).
View SolutionIf the work done in blowing a soap bubble of volume 'V' is W, then the work done in blowing a soap bubble of volume '2V' is
View SolutionA constant pressure gas thermometer has a volume of 200cc, 273.2cc and 525 .1cc at 0°C, 100°C and boiling point of sulphur respectively. The resistance possessed by a platinum wire at the same temperatures as above are 2.000Ω,2.778Ωand5.280Ω respectively. Estimate the boiling point of sulphur on the basis of the two sets of observations.
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
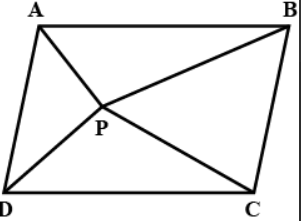
View SolutionTwo triangle ABC and DBC lie on the same side of the base BC . From a point P on BC,PQAB AND PRBD ARE DRAWN. They meet AC in Q and DC in R respectively. Prove that QRAD.
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)

View SolutionP is the centre of mass of four point masses A,B, C and D which are lying in the same length but not along the same straight line then.
View SolutionIn three dimensions there may be more than one point, which are equidistant from three given non-collinear points A, B, C. One of these points will be circumcentre of the triangle ABC.
The y-coordinate of the circumcentre of triangle ABC must be
View SolutionCalculate centre of mass of the system
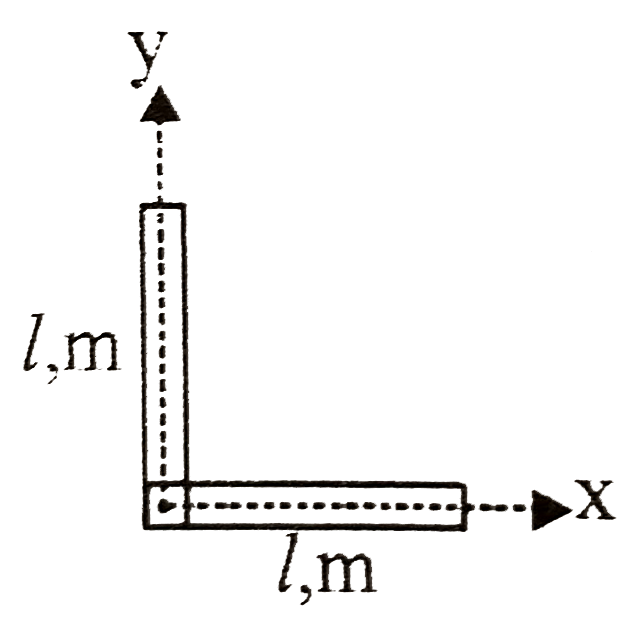
View SolutionFor positive real numbers a,bc such that a+b+c=p, which one holds? (a) (p−a)(p−b)(p−c)≤827p3 (b)(p−a)(p−b)(p−c)≥8abc (c)bca+cab+abc≤p (d) none of these
View SolutionABCD are four points in a plane and Q is the point of intersection of the lines joining the mid-points of AB and CD;BC and AD. Show that →PA+→PB+→PC+→PD=4→PQ, where P is any point.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View Solution
