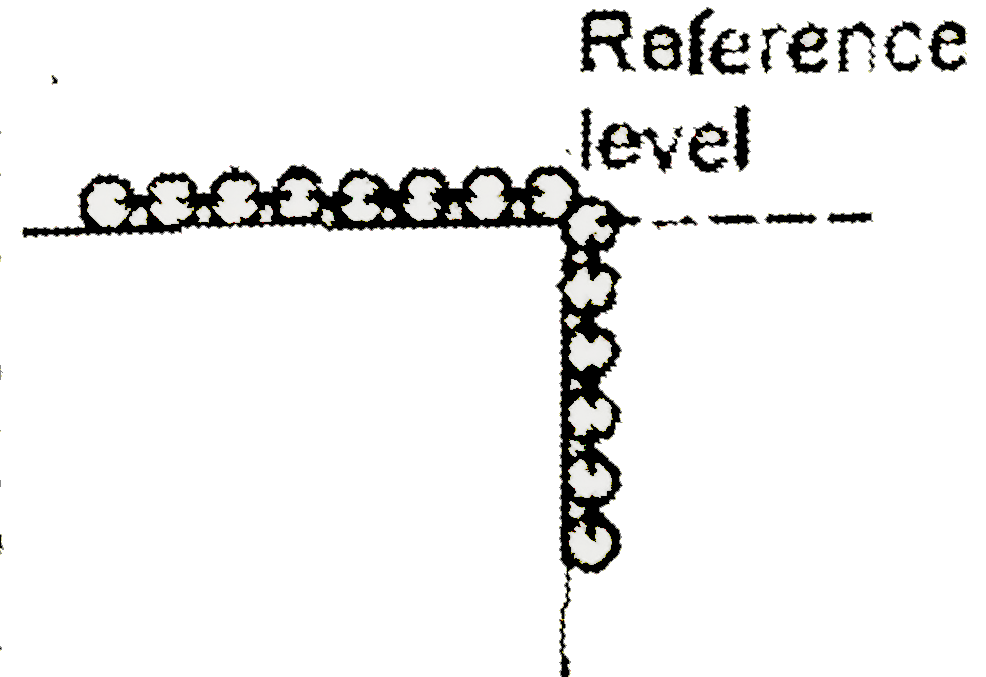
A uniform chain of length 'L' and mass 'm' is on a smooth horizontal table, with $\frac{1}{n}$ th part of its length hanging from the edge of the table. Find the kinetic energy of the chain as it completely slips off the table

Text Solution

Verified by Experts

With respect to the top of the table, the initial potential energy of the chain
$U_{1}$ = PF of the chain lying on the table + PE of the hanging part of the chain
$= L (1 - \frac{1}{n}) m g (0) \frac{m}{n} g (- \frac{L}{2 n}) = - \frac{m g L}{2 n^{2}}$
P.E of the chain, when it just slips off the table.
$U_{2} = m g (\frac{- L}{2}) = - \frac{m g L}{2}$
From law of conservation of energy
$Δ K = - Δ U K_{r} - K_{i} = - (U_{f} - U_{i})$
$∵ K_{i} = 0, K_{f} = - [- \frac{m g L}{2} - (- \frac{m g L}{2 n^{2}})]$

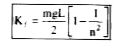
If .V. is the velocity of the chain, then, $\frac{1}{2} m v^{2} = \frac{m g L}{2} [1 - \frac{1}{n^{2}}]$

A chain is held on a frictionless table with $1 / n$ th of its length hanging over the edge. If the chain has a length L and a mass M, how much work is required to pull the hanging part back on the table?
A $M g L / 2 n^{2}$
B $2 M g L / - 2 n^{2}$
C $M g L / 4 n^{3}$
D $M g L / 3 n^{- 1}$
A uniform chain of length $l$ and mass m is placed on a smooth table with one-fourth of its length hanging over the edge. The work that has to be done to pull the whole chain back onto the table is :
A $\frac{1}{4} m g l$
B $\frac{1}{8} m g l$
C $\frac{1}{16} m g l$
D $\frac{1}{32} m g l$