इलेक्ट्रॉन व प्रोटॉन के मध्य बल हेतु स्थिर वैद्युतिकी का व्युत्क्रम वर्ग नियम है-
|F|=e2(4πε0).r2|F| की (1r) निर्भरता को क्वाण्टम सिद्धान्त में इस प्रकार समझा जा सकता है कि प्रकाश का 'कण' (फोटान) द्रव्यमान रहित है। यदि प्रोटान का द्रव्यमान mp हो तो बल का संशोधित रूप होगा।
|F|=e2(4πε0)r2[1r2+λr]e×p(−λr) जहाँ λ=mpC/h तथा ¯h=h2π
हाइड्रोजन परमाणु की न्यूनतम अवस्था की ऊर्जा में परिवर्तन का आकलन करें यदि mp इलेक्ट्रॉन के द्रव्यमान का 10−6 गुना है।
mpc2=10−6× इलेक्ट्रॉन द्रव्यमान ×c2
≈10−6×0.5MeV
≈10−6×0.5×1.610−13
≈0.8×10−19J
¯hmpc=¯hcmpc2=10−34×3×1080.8×10−19≈4×10−7m>> बोहर त्रिज्या
|F|=e24πε0[1r2+λr]exp(−λr)
जहाँ λ−1=¯hmpc≈4×10−7m>>rB
∴λ<<1rB अर्थात λrB<<1
U(r)=−e24πε0.exp(−λr)r
mvr=¯h∴v=¯hmr
यह भी :mv2r=≈(e24πε0)[1r2+λr]
∴¯h2mr3=(e24πε0)[1r2+λr]
∴¯h2m=(e24πε0)[r+λr2]
यदि λ=0,r=rB=¯hm.4πε0e2
¯h2m=e24πε0.rB
क्योंकि λ−1>>rB,r=rB+δ रखें
∴rB=rB+δ+λ(r2B+δ2+2δrB),δ2 नगण्य है |
अथवा O=λr2B+δ(1+2λrB)
δ=λr2B(1−2λrB)=−λr2B क्योंकि λrB<<1
∴V(r)=−e24πε0.exp(−λδ−λrB)rB+δ
∴V(r)=−e24πε0/1rB[(1−δrB).(1−λrB)]
≅(−27.2eV) अपरिवर्तित रहता है |
गतिज ऊर्जा =12mv2=12m.¯h2mr2=¯h22(rB+δ)2=¯h22r2B(1−2δrB)
=(13.6eV)[1+2λrB]
कुल उर्जा =e24πε0rB+h22r2B[1+2λrB]
=−27.2+13.6[1+2λrBeV=27.2λrBeV
Topper's Solved these Questions
Similar Questions
पोजीट्रोनियम, पोज़ीट्रॉन (इलेक्ट्रॉन का धनात्मक रूप से आवेशित वह प्रतिकण जो इलेक्ट्रॉन के समान ही द्रव्यमान वाला होता है) के द्वारा विस्थापित प्रोटॉन वाले H-परमाणु के समान होता है। पोजीट्रोनियम की मूल अवस्था ऊर्जा होगी-
View Solutionकभी-कभी कोई रेडियोएक्टिव नाभिक विघटित होकर एक ऐसा नाभिक बनाता है जो स्वयं भी रेडियोएक्टिव होता है, उदाहरणार्थ 38Sअधायु −−−−→=2.48h38Cl अधायु −−−−→=0.2h38Ar (स्थायी) मान लीजिए हम 1 = 0 पर 1000 S18 नाभिकों से प्रारम्भ करते हैं। 1 = 0 पर 38CI की संख्या शून्य है तथाt=∞ पर पुन: शून्य है। 1 के किस मान पर नाभिकों की संख्या अधिकतम होगी और उस समय यह संख्या क्या होगी?
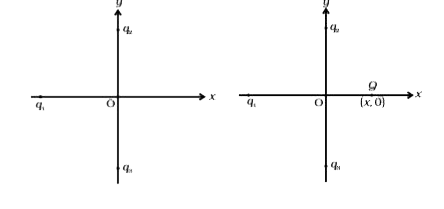
View Solutionचित्र 1.1 में y-अक्ष के अनुदिश स्थित दो वैद्युत आवेश q2 तथा q3 , X-अक्ष के अनुदिश स्थित वैद्युत आवेश q1 पर, +x दिशा में कोई नेट विद्युत बल आरोपित करते हैं। यदि (x, 0), पर कोई धनावेश Q रख दिया जाए तो q1 पर आरोपित बल
View Solutionएक इलेक्ट्रॉन (द्रव्यमान किग्रा) व एक प्रोटॉन (द्रव्यमान किग्रा) के बीच गुरुत्वाकर्षण-बल व स्थिरवैघुत बल का अनुपात ज्ञात कीजिए। (e=1.6×10−19 कूलाम तथा G=6.67×10−11 (न्यूटन-मीटर^(2)/किग्रा^(2))
View Solutionरासायनिक संयोजन के नियम || द्रव्यमान संरक्षण का नियम || स्थिर अनुपात का नियम || गुणित अनुपात का नियम || व्युत्क्रम अनुपात का नियम
View Solutionरासायनिक संयोजन के नियम || द्रव्यमान संरक्षण का नियम || स्थिर अनुपात का नियम || गुणित अनुपात का नियम || व्युत्क्रम अनुपात का नियम || उदाहरण | VIPIN CHOUBISA | CHEMISTRY
View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionरासायनिक संयोजन के नियम || द्रव्यमान संरक्षण का नियम || स्थिर अनुपात का नियम || गुणित अनुपात का नियम || व्युत्क्रम अनुपात का नियम
View Solutionरासायनिक संयोजन के नियम || द्रव्यमान संरक्षण का नियम || स्थिर अनुपात का नियम || गुणित अनुपात का नियम || व्युत्क्रम अनुपात का नियम || उदाहरण
View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
View Solutionपृथ्वी और चन्द्रमा का कुल द्रव्यमान 6.04×1024 किग्रा है। यदि चन्द्रमा का द्रव्यमान 7.34×1022 किग्रा है तो पृथ्वी का द्रव्यमान ज्ञात कीजिए।
View Solutionयदि संख्या 354Y2, 6 का एक गुणज है तो Yअंक का मान क्या हो सकता है?
View SolutionThe area of triangle ABC is 44 cm^2 . If D is the midpoint of BC and E is the midpoint of AB, then the area (in cm^2 ) of triangle BDE is: triangle ABC का क्षेत्रफल 44 वर्ग सेमी है | यदि D, BC का मध्य बिंदु है तथा E, AB का मध्य बिंदु है, तो triangle BDE का क्षेत्रफल ( वर्ग सेमी में ) होगा :
View Solutionif '+' means '_' and '-' and 'xx', 'xx' means '-:' and '-:' means '+' then 2 -: 6xx6-:2 = ? यदि '+ ' का अर्थ है । '-', '-' का अर्थ है 'xx','xx' का अर्थ है। और '-:' का अर्थ है '-:' तो 2-:6xx6-:2=?
View Solution
