What is the moment of inertia of a square sheet of side l and mass per unit area μ about an axis passing through the centre and perpendicular to its plane
μl212
μl26
μl412
μl46
The correct Answer is:D
To find the moment of inertia of a square sheet of side l and mass per unit area μ about an axis passing through the center and perpendicular to its plane, we can follow these steps:
1. Determine the Area of the Square Sheet:
The area A of the square sheet can be calculated using the formula:
A=l2
2. Calculate the Total Mass of the Square Sheet:
Given the mass per unit area μ, the total mass M of the square sheet can be calculated as:
M=μ×A=μ×l2
3. Use the Formula for Moment of Inertia:
The moment of inertia I of a square sheet about an axis passing through its center and perpendicular to its plane is given by the formula:
I=16Ml2
4. Substitute the Total Mass into the Moment of Inertia Formula:
Now, substituting the expression for M into the moment of inertia formula:
I=16(μl2)l2
5. Simplify the Expression:
Simplifying the equation gives:
I=16μl4
Final Result:
Thus, the moment of inertia of the square sheet about the specified axis is:
I=μl46
The area A of the square sheet can be calculated using the formula:
A=l2
Given the mass per unit area μ, the total mass M of the square sheet can be calculated as:
M=μ×A=μ×l2
The moment of inertia I of a square sheet about an axis passing through its center and perpendicular to its plane is given by the formula:
I=16Ml2
Now, substituting the expression for M into the moment of inertia formula:
I=16(μl2)l2
Simplifying the equation gives:
I=16μl4
Thus, the moment of inertia of the square sheet about the specified axis is:
I=μl46
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular momentum)
16 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on kinetic energy, work and power)
30 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on torque, couple)
11 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
The moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View Solution
Knowledge Check
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correctMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2The moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to plate is
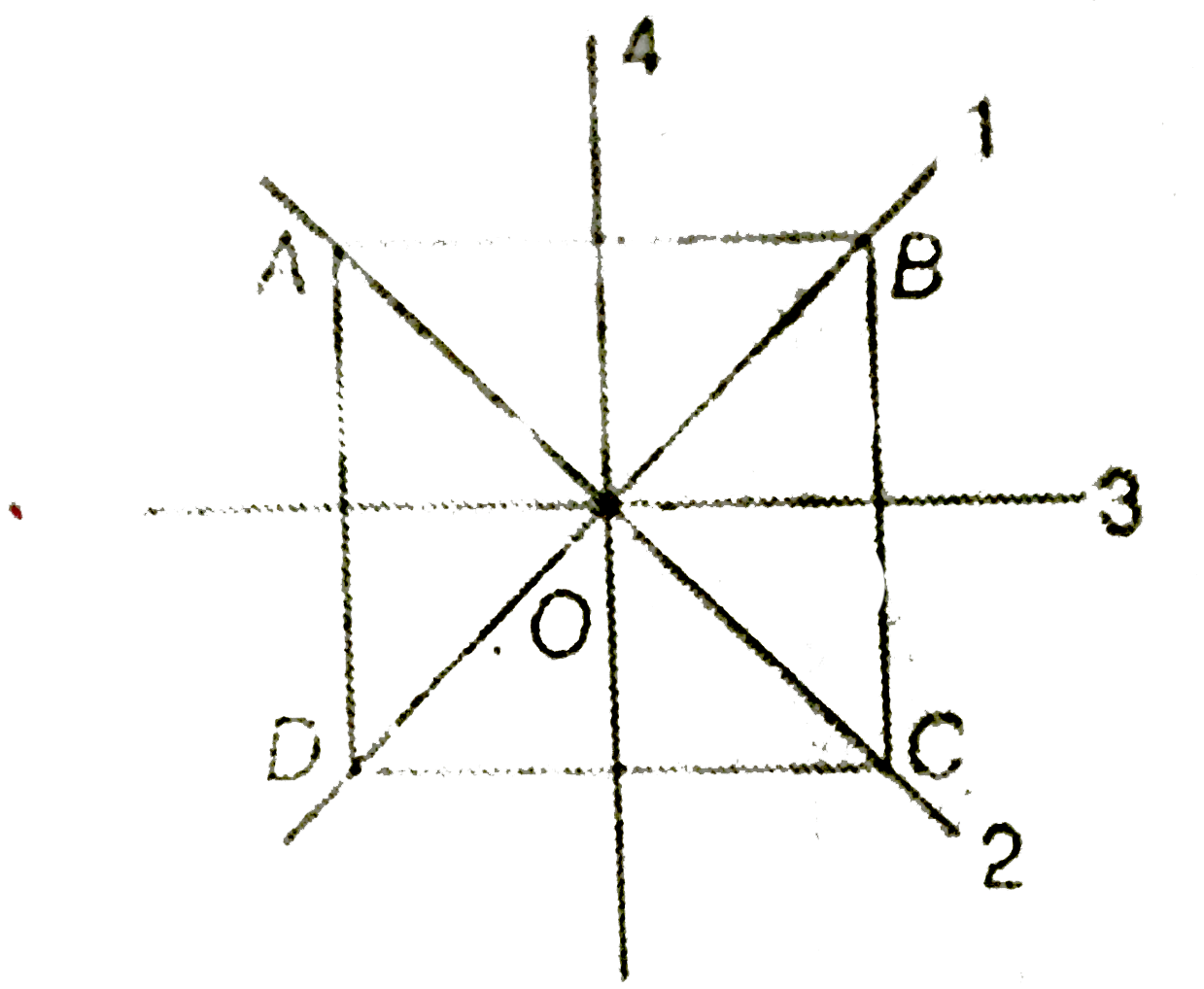 Al1+l2Bl2+l3Cl1+l3Dl3+l4
Al1+l2Bl2+l3Cl1+l3Dl3+l4
What is the moment of inertia of a ring of mass 2kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane ? Also find the moment of inertia about a parallel axis through its edge.
View SolutionCalculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through its center and perpendicular to its plane will

View SolutionThe moment of inertia of a rod of length l about an axis passing through its centre of mass and perpendicular to rod is I. The moment of inertia of hexagonal shape formed by six such rods, about an axis passing through its centre of mass and perpendicular to its plane will be
View SolutionThe moment of inertia of a rod of length l about an axis passing through its centre of mass and perpendicular to rod is I. The moment of inertia of hexagonal shape formed by six such rods, about an axis passing through its centre of mass and perpendicular to its plane will be
View Solution
