The moment of inertia of $H C l$ molecule about an axis passing through its centre of mass and perpendicular to the line joining the $H^{+}$ and $C l^{-}$ ions will be (if the inter atomic distance is $1 A^{\circ}$ )

A

$0.61 \times 10^{- 47} k g . m^{2}$

B

$1.61 \times 10^{- 47} k g . m^{2}$

C

$0.061 \times 10^{- 47} k g . m^{2}$

D

0

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

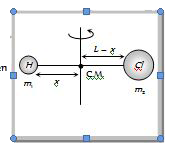
If $r_{1}$ and $r_{2}$ are the respective distances of particles $m_{1}$ and $m_{2}$ from the centre of mass then
$m_{1} r_{1} = m_{2} r_{2} \Rightarrow 1 \times x = 35.5 \times (L - x) \Rightarrow x = 35.5 (1 - x)$
$\Rightarrow x = 0.973 Å and L - x = 0.027 Å$
Moment of inertia of the system about centre of mass $I = m_{1} x^{2} + m_{2} {(L - x)}^{2}$
$I = 1 amu \times {(0.973 Å)}^{2} + 35.5 amu \times {(0.027 Å)}^{2}$
Substituting 1 a.m.u. = $1.67 \times 10^{- 27} k g and 1 Å = 10^{- 10} m$
$l = 1.62 \times 10^{- 47} k g m^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increased
Bchanges if its axis of rotation is changed
Cincreases if its angular velocity is increased
Dboth (a) and (b) are correct
Question 2 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A $1 / 2 M R^{2}$
B $M R^{2}$
C $1 / 4 M R^{2}$
D $3 / 4 M R^{2}$
Question 3 - Select One
Moment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
A $I = \frac{1}{2} M R^{2}$
B $I = M R^{2}$
C $I = \frac{3}{2} M R^{2}$
D $I = \frac{5}{2} M R^{2}$

ERRORLESS -ROTATIONAL MOTION-Practice Problems (Problems based on motion of connected mass)

Home
Ask Doubt
Profile