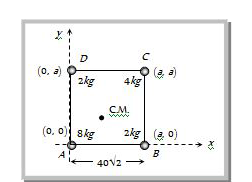
4 Masses 8 kg, 2 kg, 4 kg and 2 kg are placed at the corners A, B, C, D respectively of a square ABCD of diagonal 80 cm. The distance of centre of mass from A will be
20 cm
30 cm
40 cm
60 cm
The correct Answer is:B
Let corner A of square ABCD is at the origin and the mass 8 kg is placed at this corner (given in problem) Diagonal of square d=a√2=80cm⇒a=40√2cm
m1=8kg,m2=2kg,m3=4kg,m4=2kg
Let →r1,→r2,→r3,→r4 are the position vectors of respective masses
→r1=0ˆi+0ˆj,→r2=aˆi+0ˆj,→r3=aˆi+aˆj,→r4=0ˆi+aˆj
From the formula of centre of mass
→r=m1→r1+m2→r2+m3→r3+m4→r4m1+m2+m3+m4=15√2i+15√2ˆj
∴ co-ordinates of centre of mass =(15√2,15√2) and co-ordination of the corner = (0, 0)
From the formula of distance between two points (x1,y1) and (x2,y2)
distance =√(x2−x1)2+(y2−y1)2=√(15√2−0)2+(15√2−0)2=√900=30cm
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on centre of mass)
12 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular displacement, velocity and acceleration)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
3Masses 8 kg, 2 kg, 4 kg and 2 kg are placed at the corners A, B, C, D respectively of a square ABCD of diagonal 80 cm. The distance of centre of mass from A will be
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View Solution
Knowledge Check
Point masses of 2 kg, 3 kg, 5 kg and 7 kg are placed at the corners of a square ABCD respectively whose each side is 1 m long. The position of the centre of mass of the system is
A1417m,817mB1217m,1017mC1517m,1017mD1217m,817mFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
A(0.5,0.3)B(0.4,0.3)C(0.5,0.8)D(0.7,0.3)Particles of masses 3 kg, 4 kg, 5 kg nd 2 kg are placed at points A(3,2),B(−2,2),C(−2,−3) and D(1,−2) respectively of a co-ordinate system. The centre of mass of the system is at
A(−12,−12)B(−12,−514)C(0,−12)D(0,0)
Four particles of masses 1kg,2kg,3kg and 4kg are placed the four vertices A,B,C and D, respectively, of a square of side 1m. Find the position of centre of mass of the particles.
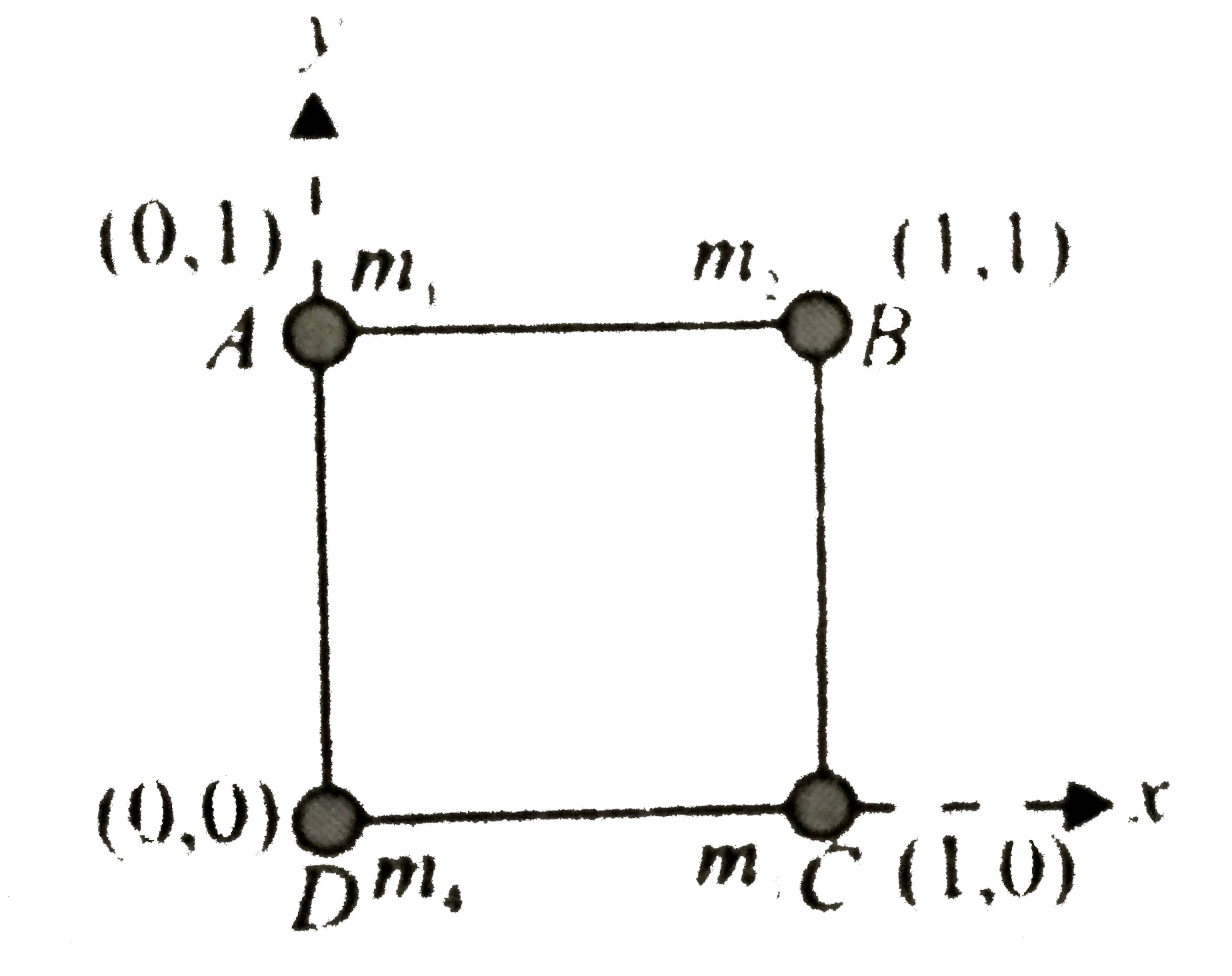
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A,B,C and D of a square of side 1m. Find square of distance of their centre of mass from A.
View SolutionParticle of masses 2 kg, 2 kg, 1 kg and 1 kg are placed at the corners A, B, C, D of a square of side L as shown in Fig. Find the centre of mass of the system.

View SolutionThree particles of msses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre ofmass of the system.
View SolutionFour particles of masses 1 kg, 2 kg, 3 kg, 4 kg are placed at the corners of a square of side 2 m. Find the coordinates of centre of mass.
View Solution
