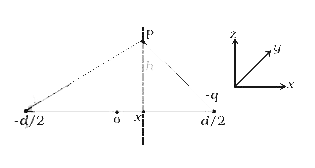
+q तथा -q परिमाण के दो बिन्दु आवेश क्रमशः (-d/2, 0,0) तथा (d/2, 0,0) पर स्थित हैं। उस समविभव पृष्ठ के लिए समीकरण प्राप्त कीजिए जहाँ विभव शून्य है।
मान लीजिए तल मूल बिन्दु से दुरी x है। तब बिन्दु P पर विभव है।
14πε0q[(x+d/2)2+h2]1/2−14πε0q[(x−d/2)2+h2]1/2
यदि यह विभव शून्य है, तो
1[(x+d/2)2+h2]1/2=1[(x−d/2)2+h2]1/2
अथवा (x−d/2)2+h2=(x+d/2)2+h2
⇒x2−dx+d2/4=x2+dx+d2/4
Or, 2dx=0
⇒x=0 यह तल x =0 का समीकरण है
Topper's Solved these Questions
Similar Questions
सिद्ध कीजिए कि किसी ऐसे बन्द समविभव पृष्ठ, जिसके भीतर कोई आवेश नहीं है, में कोई समविभव आयतन परिबद्ध होना चाहिए।
View Solutionकिसी संचार चैनल के अनुदिश गतिशील प्रकाश स्पन्द की तीव्रता, दूरी के साथ चरघातांकी रूप से, निम्न संबंध के अनुसार घटती है, I=I0e−αx जहाँ I0.x=0 पर तीव्रता है तथा α क्षीणन नियतांक है। दिखाइये कि (In4α) दूरी तय करने के पश्चात् तीव्रता में 75% की कमी आ जाती है।
View Solutionकिसी निकाय में दो आवेश qA=2.5×10−7C तथा qB=−2.5×10−7C क्रमश: दो बिंदुओं A:(0,0,−15cm) तथा B:(0,0,+15) पर स्थित है। निकाय का कुल आवेश तथा विद्युत द्विध्रुव आघूर्ण क्या है?
View Solutionएक रेखा के कार्तीय समीकरण 6x−2=3y+1=2z−2 है। रेखा के दिक्-अनुपात ज्ञात कीजिए तथा बिन्दु (2,−1,−1) से गुजरने वाली उस रेखा का सदिश समीकरण लिखिए जो दी हुई रेखा के समान्तर है।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज के शीर्षो के निर्देशांक (2,5),(6−2) तथा (−3,−4) है , तो उसकी मध्यिकाओ के समीकरण ज्ञात कीजिए
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionफलन f(x)=x2−4xx+2 के लिए अंतराल [0,4] में रोले प्रमेय का सत्यापन कीजिए तथा वह बिंदु ज्ञात कीजिए जहाँ अवकलन शून्य है।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionयदि बिन्दु (2,α,β) उस समतल पर स्थित है, जो बिन्दुओ (3,4,2) तथा (7,0,6) से होकर जाता है तथा समतल 2x−5y=15 के लंबवत है, तो 2α−3β बराबर है
View Solutionउस सरल रेखा का समीकरण जो रेखाओं 3x-y+ 2 = 0 तथा 5x-2y+ 7 = 0 के प्रतिच्छेद बिन्दु से गुजरती है तथा जिसकी प्रवणता अनन्त है, होगा
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View Solutionकिसी बिन्दु-आवेश के कारण तथा आवेशों के निकाय के कारण विद्युत् क्षेत्र
View Solutionबिन्दु-आवेशों के समूह के कारण विद्युत विभव || समविभव पृष्ठ, || विभव प्रवणता : विभव-प्रवणता तथा विद्युत क्षेत्र की तीव्रता में सम्बन्ध,
View Solution
