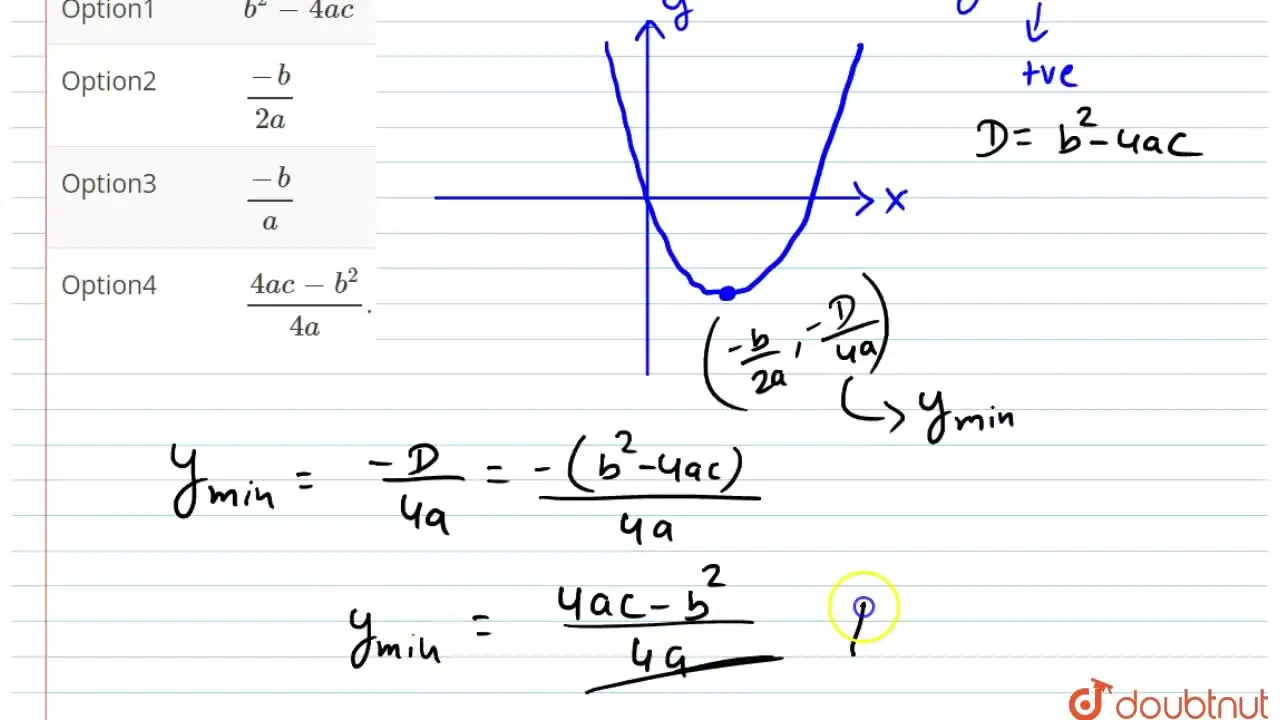
The least value of ax2+bx+c,(a>0) is
b2−4ac
−b2a
−ba
4ac−b24a.
The correct Answer is:D
Step by step video & image solution for The least value of ax^2+bx+c,(a>0) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
If ax2+bx+10=0 does not have two distinct real roots, then the least value of 5a + b, is
View SolutionIf ax2−bx+c=0 have two distinct roots lying int eh interval (0,1),a,b,ceπslonN The least value of log5abc is
View SolutionIf ax+1bx=c, then the value of bx+1ax is :
View SolutionThe equations x2+3x+5=0and ax2+bx+c=0 have a common root. If a,b,c∈N then the least possible values of a+b+c is equal to
View SolutionIf one root of the equation ax2+bx+c=0 is −92(a,b,c being positive integers) and b4c=ab, is then least value of (a+c) is equal to
View SolutionIf a−b,b−c are the roots of ax2+bx+c=0 then the value of (a−b)(b−c)c−a ,is
View SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of c isView SolutionIf ax2+bx+c=0 have two distinct roots lying int eh interval (0,1),a,b,c εN The least value of b is
View SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of b isView SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of a isView Solution