A small wooden block of density 400kg/m3 is released from rest inside a swimming pool filled with water of density 103kg/m3. The acceleration of the block just after it is released is __________ m/s2(g=10m/s2)
The correct Answer is:15
To find the acceleration of the wooden block just after it is released in water, we can follow these steps:
Step 1: Identify the Given Data
- Density of the wooden block, ρb=400kg/m3
- Density of water, ρw=1000kg/m3
- Acceleration due to gravity, g=10m/s2
Step 2: Determine the Forces Acting on the Block
When the block is submerged in water, two main forces act on it:
1. The weight of the block (W) acting downwards:
W=mg=ρbVg
where V is the volume of the block.
2. The buoyant force (Fb) acting upwards, which is equal to the weight of the water displaced by the block:
Fb=ρwVg
Step 3: Calculate the Net Force Acting on the Block
The net force (Fnet) acting on the block can be calculated as:
Fnet=Fb−W
Substituting the expressions for Fb and W:
Fnet=ρwVg−ρbVg
Factoring out Vg:
Fnet=Vg(ρw−ρb)
Step 4: Apply Newton's Second Law
According to Newton's second law, the net force is also equal to the mass of the block times its acceleration (a):
Fnet=ma
The mass of the block (m) is given by:
m=ρbV
Thus, we can write:
Vg(ρw−ρb)=ρbVa
Step 5: Simplify the Equation
Dividing both sides by V (assuming V≠0):
g(ρw−ρb)=ρba
Now, solving for a:
a=g(ρw−ρb)ρb
Step 6: Substitute the Values
Substituting the known values:
a=10m/s2×(1000kg/m3−400kg/m3)400kg/m3
a=10m/s2×600kg/m3400kg/m3
a=6000m/s2400
a=15m/s2
Final Answer
The acceleration of the block just after it is released is 15m/s2.
---
- Density of the wooden block, ρb=400kg/m3
- Density of water, ρw=1000kg/m3
- Acceleration due to gravity, g=10m/s2
When the block is submerged in water, two main forces act on it:
1. The weight of the block (W) acting downwards:
W=mg=ρbVg
where V is the volume of the block.
2. The buoyant force (Fb) acting upwards, which is equal to the weight of the water displaced by the block:
Fb=ρwVg
The net force (Fnet) acting on the block can be calculated as:
Fnet=Fb−W
Substituting the expressions for Fb and W:
Fnet=ρwVg−ρbVg
Factoring out Vg:
Fnet=Vg(ρw−ρb)
According to Newton's second law, the net force is also equal to the mass of the block times its acceleration (a):
Fnet=ma
The mass of the block (m) is given by:
m=ρbV
Thus, we can write:
Vg(ρw−ρb)=ρbVa
Dividing both sides by V (assuming V≠0):
g(ρw−ρb)=ρba
Now, solving for a:
a=g(ρw−ρb)ρb
Substituting the known values:
a=10m/s2×(1000kg/m3−400kg/m3)400kg/m3
a=10m/s2×600kg/m3400kg/m3
a=6000m/s2400
a=15m/s2
The acceleration of the block just after it is released is 15m/s2.
Similar Questions
Knowledge Check
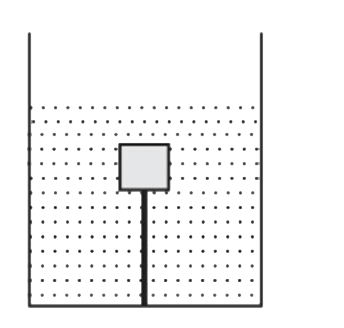
A wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
 A2NB3NC5ND6N
A2NB3NC5ND6NA wooden block of density 860kg/m3 at 0∘C is floating on bezene liquid of density 900kgm3 at 0∘C. The temperature at which the block just submerge in benzene is
[γwood=8×10−5/∘c,γbenzene=12×10−4/∘c]A24∘cB42∘cC16∘cD32∘cA sphere of radius 10cm and density 500kg/m3 is under water of density 1000kg/m3 The acceleration of the sphere is 9.80m/s2 upward viscosity of water is 1.0 centipoise if g=9.81m/s2 the velocity of the sphere is
A9m/sB10m/sC11m/sD12m/s
A block of mass 5 kg and volume 0.05m3 floats in a liquid of density 140kg m−3 .
The fraction of block inside liquid is
View SolutionA 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)

View SolutionIf the density of a block is 981 kg/m3 then it shall
View SolutionA tank with length 10 m, breadth 8 m and depth 6 m is filled with water upto top . If G=10m/s2. And density of water =1000kg/m3, then the thrust on the bottom is:
View SolutionA small block of wood of relative density 0.5 is submerged in water at a depth of 5 m When the block is released it starts moving upwards, the acceleration of the block is (g=10ms−2)
View Solution