In a circle with centre 'O' PA and PB are two chords. PC is the chord that bisects the angle . APB The tangent to the circle at C is drawn meeting PA and PB extended at Q and R respectively. If QC = 3, QA = 2 and RC = 4, then length of RB equals a/b where a and b are co-prime then a+b is_______.
The correct Answer is:11
To solve the problem, we will follow a step-by-step approach using the properties of tangents and angle bisectors in circles.
Step 1: Understand the Geometry
We have a circle with center O, and two chords PA and PB. The chord PC bisects the angle APB. A tangent is drawn at point C, which intersects the extensions of PA and PB at points Q and R, respectively.
Step 2: Use the Tangent-Chord Theorem
According to the tangent-chord theorem, the square of the length of the tangent segment (QC) from point Q to point C is equal to the product of the lengths of the segments of the chord (QA and QB):
QC2=QA⋅QB
Given:
- QC=3
- QA=2
We can find QB:
QC2=32=9
9=2⋅QB⟹QB=92
Step 3: Apply the Angle Bisector Theorem
In triangle PQR, since PC is the angle bisector, we can use the angle bisector theorem, which states:
PQPR=QCCR
Given:
- QC=3
- CR=4
- PQ=QB=92
Let PR=x. Then we can set up the equation:
92x=34
Cross-multiplying gives:
3x=4⋅92
3x=18⟹x=6
So, PR=6.
Step 4: Use the Tangent-Chord Theorem Again
Now we will apply the tangent-chord theorem again for point R:
RC2=RB⋅RP
Given:
- RC=4
- RP=PR=6
Thus, we have:
42=RB⋅6
16=RB⋅6⟹RB=166=83
Step 5: Express RB in the Form a/b
We can express RB as:
RB=83
Here, a=8 and b=3, which are co-prime.
Final Step: Calculate a + b
Now, we need to find a+b:
a+b=8+3=11
Thus, the final answer is:
11
We have a circle with center O, and two chords PA and PB. The chord PC bisects the angle APB. A tangent is drawn at point C, which intersects the extensions of PA and PB at points Q and R, respectively.
According to the tangent-chord theorem, the square of the length of the tangent segment (QC) from point Q to point C is equal to the product of the lengths of the segments of the chord (QA and QB):
QC2=QA⋅QB
Given:
- QC=3
- QA=2
QC2=32=9
9=2⋅QB⟹QB=92
In triangle PQR, since PC is the angle bisector, we can use the angle bisector theorem, which states:
PQPR=QCCR
Given:
- QC=3
- CR=4
- PQ=QB=92
92x=34
3x=4⋅92
3x=18⟹x=6
So, PR=6.
Now we will apply the tangent-chord theorem again for point R:
RC2=RB⋅RP
Given:
- RC=4
- RP=PR=6
42=RB⋅6
16=RB⋅6⟹RB=166=83
We can express RB as:
RB=83
Here, a=8 and b=3, which are co-prime.
Now, we need to find a+b:
a+b=8+3=11
11
Similar Questions
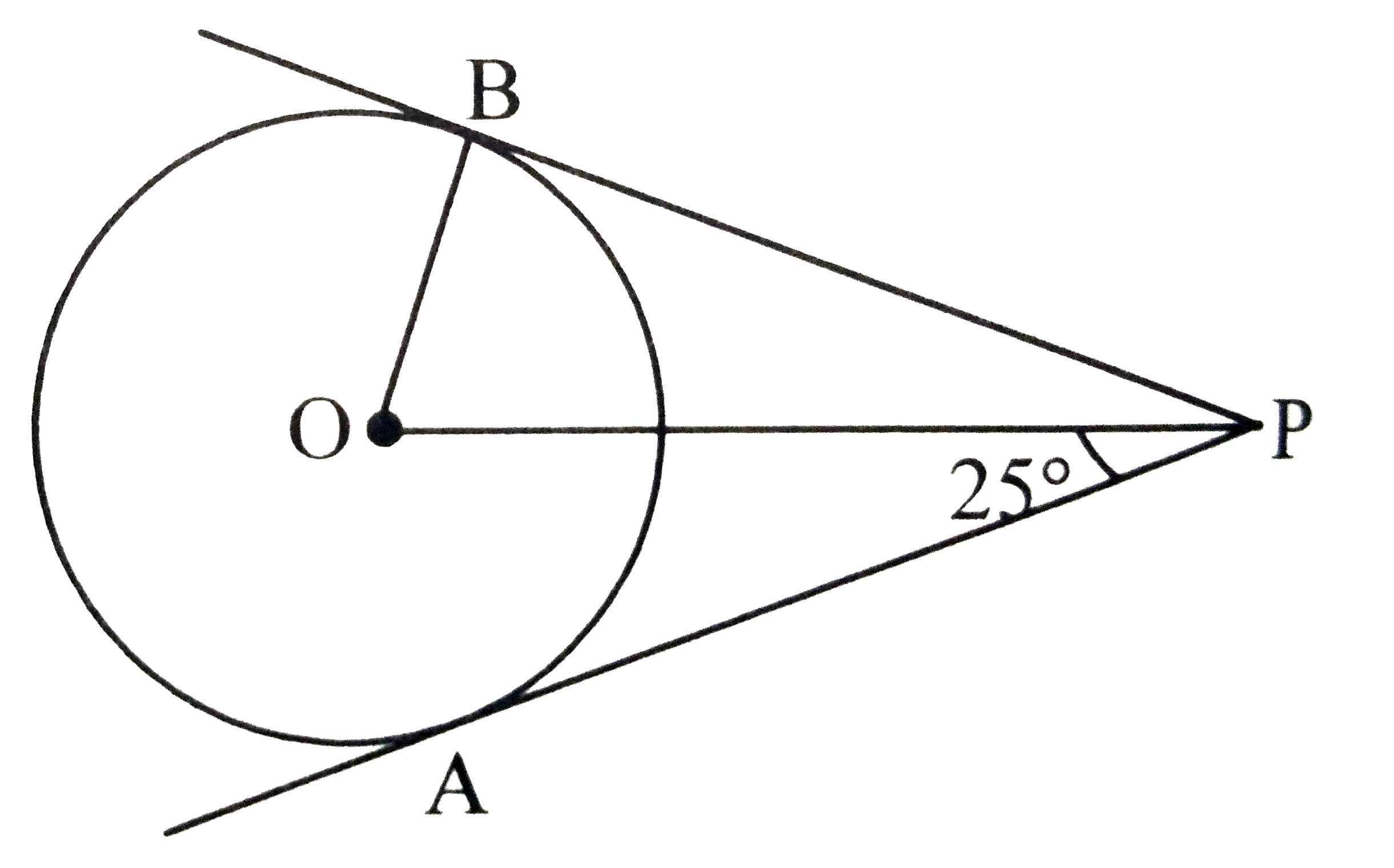
PA and PB are tangents to the circle with centre O touching it at A and B respectively. IF ∠APO=25∘ , then ∠POB is
View SolutionFrom an external point P, two tangents, PA and PB are drawn to a circle with centre 0. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA=10 cm, find the perimeter of the triangle PCD.
View Solution
Knowledge Check
From a point P outside the circle with centre O, two tangents PA and PB are drawn to meet the circle at A and B respectively. If ∠APB=70∘, then ∠OAB is equal to :
केंद्र O वाले वृत्त के बाहर स्थित किसी बिंदु P से दो स्पर्श रेखाएं PA और PB खींची जाती हैं जो वृत्त से क्रमशः A और B मिलती हैं | यदि ∠APB=70∘ है, तो कोण OAB का मान ज्ञात करें |A35∘B65∘C45∘D55∘If PA and PB are tangents to the circle with centre O such that ∠APB=50∘ then ∠OAB is equal to
A50∘B30∘C40∘D25∘In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
A36∘B18∘C27∘D36∘
From an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D which intersect PA and PB at point E and C respectvely. If AP=15 cm, find the permeter of the △PEC.
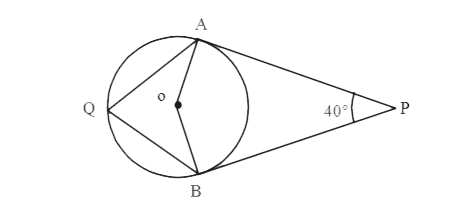
View SolutionIn the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find ∠AQB.
View SolutionPAandPB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN=AK+BN.
View SolutionFrom an external point P , tangents PA and PB drawn to a circle with centre O . If CD is the tangent to the circle at a point E and PA=14cm , find the perimeter of PCD .
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If ∠APB=30∘, then ∠OAB is equal to :
View Solution
