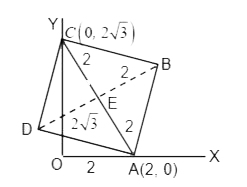
One diagonal of a square is the portion of the line √3x+y=2√3 intercepted by the axes. Obtain the extremities of the other diagonal is : (A) (1+√3,−1+√3) (B) (1+√3,1+√3) (C) (1−√3,−1+√3) (D) (1−√3,1+√3)
A
(1+√3,√3−1)
B
(1+√3,−√3+1)
C
(1−√3,√3−1)
D
(1−√3,√3+1)
Video Solution
Text Solution
The correct Answer is:C
Clearly, OA=2,OC=2√3 ∴ E=(1,√3).
Also, AC=√22+2(√3)2=4 ∴ EB=ED=12AC=2
.m. of AC=−√3
∴ .m. of BD=1√3=tan30∘
∴ B or D=(1±2.cos30∘,√3±2.sin30∘).
|
Similar Questions
Knowledge Check
The value of 2+√32−√3+2−√32+√3+√3+1√3−1 is
A16+√3B4−√3C2−√3D2+√3√2−1√2+1+√2+1√2−1√3−1√3+1+√3+1√3−1 equals:
A23B4C32D6
