The position vectors of vertices of △ABC are (1,−2),(−7,6)and(115,25) respectively. The measure of the interior angle A of the △ABC, is,
A
acute and lies in (75∘,90∘)
B
acute and lies in (60∘,75∘)
C
acute and lies in (45∘,60∘)
D
obtuse and lies in (120∘,150∘)
Video Solution
Text Solution
The correct Answer is:B
tan(θ2−θ1)=m2−m11+m1m2=8−6−21−166
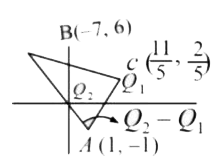
tanθ=2010=2
|
Similar Questions
Knowledge Check
The vertices of a triangle ABC are (1,1),(4,-2) and (5,5) respectively. Then equation of perpendiculart dropped from C to the internal bisector of angle A is
Ay−5=0Bx−5=0C2x+3y−7=0DnoneThe vertices of the triangle ABC are A(1, 2), B (0, 0) and C (2, 3), then the greatest angle of the triangle is
A75∘B105∘C120∘Dnone of theseThe midpoints of the sides of triangle ABC are (-1,-2) , (6,1) and (3,5) . The are of ΔABC is
A72 sq. unitsB73 sq. unitsC74 sq. unitsD75 sq. units
The vertices of a triangle ABC are (2,1), (5,2) and (3,4) respectively. The circumcentre is the point
View SolutionThe vertices of a triangle ABC are (2,1),(5,2) and(3,4) respectively. The circumcentre is the point
View SolutionIf the position vectors of the vertices a, B and C of a Tri∠ABC be (1,2,3),(−1,0,0) and (0,1,2) respectively then find ∠ABC.
View SolutionIf the coordinates of the vertices of triangle ABC are (−1,6),(−3,−9) and (5,−8) , respectively, then find the equation of the median through C.
View SolutionThe vertices of a triangle are A(−1,−7), B(5,1) and C(1,4). The equation of the internal bisector of the angle ∠ABC is
View Solution

