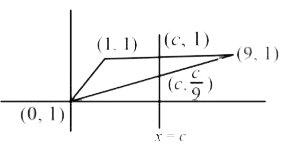
The line x = c cuts the triangle with corners (0,0) , (1,1) and (9,1) into two regions .For the area of the two regions to the same , then c must be equal to
5/2
3 only
7/2
3 or 15
The correct Answer is:B
Area of Δ=12×8×1=4
Area of small Δle=12(9−c)×(1−c9)=2
(a−c)2=36⇒9−c=6 or −6
c = 3
Similar Questions
The line x=c cuts the triangle with corners (0,0),(1,1) and (9,1) into two region. two regions to be the same c must be equal to (A) 52 (B) 3 (C) 72 (D) 5 or 15
View SolutionLet T be the triangle with vertices (0,0),(0,c2)and(c,c2) and let R be the region between y=cxandy=x2 where c>0 then
View Solution
Knowledge Check
If a △ABC has vertices (0,0), (11,60) and (91,0). If the line y=kx cuts the triangle into two triangles of equal area , then k is equal to
A3051B47C74D3091The area of the triangle formed by A (1, 0, 0), B(0, 1, 0), C(1, 1, 1) is
A12B√34C√32D14Consider a triangle ABC in the xy -plane with vertices A = (0,0), B = (1,1) and C = (9, 1). If the line x = a divides the triangle into two parts of equal area, then a equals
A3B3.5C4D4.5
Two vertices of triangle are (-2,-1) and (3,2) and third vertex lies on the line x+y=5. If the area of the triangle is 4 square units, then the third vertex is a. (-0,50 or (4,1) b. (5,0) of (1,4) c. (5,0) or (4,1) d. (o,5) or (1,4)
View SolutionFind the area of the region bounded by the curve xy=1 and the lines y=x,y=0,x=e
View SolutionThe area of the region bounded by y2=2x+1andx−y−1=0 is
View SolutionStatement 1 : The area of the triangle formed by the points A(1000,1002),B(1001,1004),C(1002,1003) is the same as the area formed by the point A′(0,0),B′(1,2),C′(2,1) Statement 2 : The area of the triangle is constant with respect to the translation of axes.
View SolutionThe line y=x+1 divided the area the curves y=cosx,[−π2,π2] and the x-axis into two regions which are in the ratio
View Solution

