A wooden block of mass M rests on a horizontal surface. A bullet of mass m moving in the horizontal direction strikes and gets embedded in it. The combined system covers a distance x on the surface. If the coefficient of friction between wood and the surface is μ , the speed of the bullet at the time of striking the block is (where m is mass of the bullet)
√2Mgμm
√2μMgMx
√2μgx(M+mm)
√2μmxM+m
The correct Answer is:C

Let speed of the bullet = v
Speed of the system after the collision = V
By conservation of momentum mv = (m+M) V
⇒VmvM+m
So the initial K.E. acquired by the system
=12(M+m)V2=12(m+M)(mvM+m)2=12m2v22(m+M)
This kinetic energy goes against friction work done by friction
=μR×x=μ(m+M)g×x
By the law of conservation of energy
12m2v2(m+M)=μ(m+M)g×x⇒v2=2μgx(m+Mm)2
∴v=√2μgx(M+mm)
Topper's Solved these Questions
- WORK , ENERGY , POWER AND COLLISIONBook:ERRORLESS Chapter:WORK , ENERGY , POWER AND COLLISIONExercise:Assertion & Reason For AIIMS Aspirants
Explore 30 Videos
- WAVES AND SOUNDBook:ERRORLESS Chapter:WAVES AND SOUNDExercise:SET
Explore 25 Videos
- WORK, ENERGY, POWER & COLLISIONBook:ERRORLESS Chapter:WORK, ENERGY, POWER & COLLISIONExercise:Assertion
Explore 30 Videos
Similar Questions
A bullet of mass 10 gram is fired horizontally into a 5 kg wooden block at rest on a horizontal surface The coefficient of kinetic friction between the block and the surface is 0.1 Calculate the speed of the bullet striking the block if the combination moves 20 m before coming rest .
View SolutionA block of mass m rests on a rough horizontal surface (Coefficient of friction isµ). When a bullet of mass m/2 strikes horizontally, and get embedded in it, the block moves a distance d before coming to rest. The initial velocity of the bullet is k√2μgd, then the value of k is
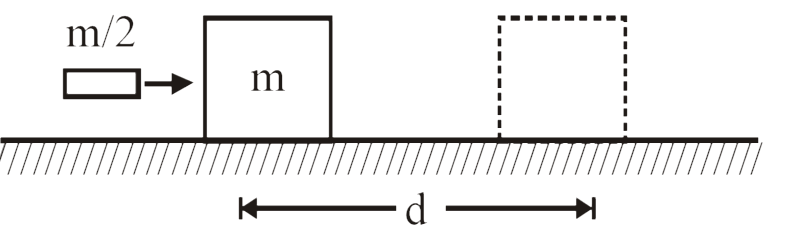
View Solution
Knowledge Check
A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A12mv2×m(m+M)B12mv2×M(m+M)C12mv2×(M+m)mD12Mv2×m(m+M)A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A12mv2×m(m+M)B12mv2×M(m+M)C12mv2×(M+m)MD12mv2(M+m)m
Find the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.

View SolutionA bullet of mass m travelling with a speed v hits a block of mass M initially at rest and gets embedded in it. The combined system is free to move and there is no other force acting on the system. The heat generated in the process will be
View SolutionA force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
View SolutionA bullet of mass in travelling with a speed v hits a block of mass M initially at rest and gets embedded in it. The combined system is free to move and there is no other force acting on the system. The heat generated in the process will be
View SolutionA circular hoop of mass m and radius R rests flat on a horizontal frictionless surface A bullet also of mass m and moving with a velocity v strikes the hoop and gets embedded in it the thickness of the hoop is much smaller then R the angular velocity with which the system rotates after the bullet strikes the hoop is

View Solution

