Obtain the expression for fringe width in the case of interference of light waves.Solution in Kannada
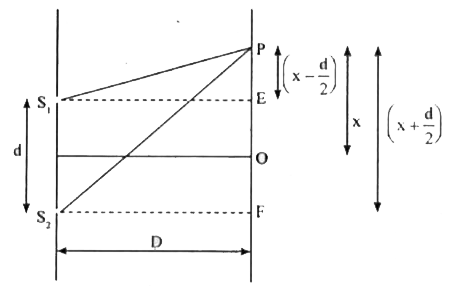
Consider two coherent sources S1 and S2 separated by a distance .d.. Let a screen be placed at a distance .D. from the coherent sources. The point .O. on the screen is equidistant from S1 and S2 . So that path difference between the two light waves from S1 and S2 reaching O is zero. Thus the point o has maximum intensity. Consider point .P. at a distance .x. from O.. The path difference between the light waves from S1 and S2 reaching point P is
δ=S2P−S1P
From the figure ΔleS2PF
(S2P)2=(S2F)2+(FP)2
=D2+(x+d2)2
Similarly ΔleS1PE
(S1P)2=(S1E)2+(EP)2
=D2+(x−d2)2
(S2P)2−(S1P)2=[D2+(x+d2)2]−[D2+(x−d2)2]=[D2+x2+d24+2(x)(d2)]−[D2+x2+d24−2(x)(d2)]
(S2P)2−(S1P)2−2xd
or S2P−S1P=2xd(S2P+S1P)
Since .P. is very close to O and d < < D
S2P+S1P≈2D
∴ Path difference : S2P−S1P=2xd2D=xdD→(1)
Equation (1) represents the path difference between light waves from S1 and S2 superposing at point P.
For bright fringe or maximum intensity at P.
S2P−S1P=nλ n=0,1,2,3.......
From eqn(1) xdD=nλ
or x=nλDd
The distance of the nth bright fringe from the centre .O. of the screen is
xn=n(λDd)
The distance of the (n+1)th bright fringe from the centre .O. of the screen is
xn+1=(n+1)(λDd)
By definition of fringe width
β=xn+1−xn
=(n+1)(λDd)−n(λDd)
λDd(n+1−n)
β=λDd
Topper's Solved these Questions
- II PUC PHYSICS (P.U. BOARD LATEST MODEL QUESTION PAPER -1)Book:SUNSTAR PUBLICATIONChapter:II PUC PHYSICS (P.U. BOARD LATEST MODEL QUESTION PAPER -1)Exercise:PART-C
Explore 8 Videos
- II PUC PHYSICS (ANNUAL EXAM QUESTIONS PAPER MARCH - 2014)Book:SUNSTAR PUBLICATIONChapter:II PUC PHYSICS (ANNUAL EXAM QUESTIONS PAPER MARCH - 2014)Exercise:PART - D
Explore 11 Videos
- II PUC PHYSICS (SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2018)Book:SUNSTAR PUBLICATIONChapter:II PUC PHYSICS (SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2018)Exercise:PART - D
Explore 10 Videos
Similar Questions
Mention any three properties of an electric charge.
View SolutionState Gauss's theorem. Obtain an expression for elactric field at any point outside a charged spherical hollow conductor (shell).
View SolutionWrite the expression for electric field intensity at any point outside and inside due to a charged spherical shell.
View SolutionIn a YDSE setup interference fringes are obtained by sodium light of wavelength 5890Å. On screen the fringes have an angular width 0.20∘. Now the wavelength of light is changed and it is found that fringe width increases by 10%, the new wavelength of incident light is :
View SolutionObtain an expression for path difference and frinage width of interfereance pattern in Young's double slit experiment. Show that the fring width is same for consecutive bright and dark bands.
The refractive indices of glass and water w.r.t. air are 32and43 respectively. Determine the refractive index of glass w.r.t. water.
View Solutionप्रकाश तरंगों के व्यतिकरण को परिभाषित कीजिए।
व्यतिकरण फ्रिंज प्रतिरूप उत्पन्न करने के लिए यंग द्विस्लिट प्रयोग का चित्र बनाइए । प्रदीप्त फ़्रिंजों के लिए फ़्रिंजों के लिए फ्रिंज चौड़ाई के व्यंजक के व्युत्पत्ति कीजिए।
View SolutionFringe width of an interference fringe is y for the two given waves. If the frequency of the source becomes double then the fringe width have been
View SolutionObtain the expression for fringe width in the case of interference of light waves.
View SolutionObtain the expression for fringe width of interference fringes in Young's double slit experiment.
View SolutionDefine fringe width in interference and derive its expression.
View SolutionObtain the expression for fringe width in the case of interference of light waves.
View SolutionAnswer the following: With a diagram showing the Young's arrangement for producing 'a sustained interference pattern, obtain the expression for the width of the interference fringes obtained in this pattern.
View SolutionObtain the expression for fringe width in the case of interference of light waves.
View SolutionDerive an expression for fringe width in Young's double slit interference of light.
View SolutionDescribe Young.s double slit experiment for the interference of light. Obtain the expression for fringe width.
View Solution

