सीमायें जो अनिधार्य रूप 1^(oo),0^@,oo^(@) रखती है , को हल करने क लिए

यदि $y = \frac{a + b x^{3 / 2}}{x^{5 / 4}}$ हो तथा $\frac{d y}{d x} = 0, x = 5$ पर विलुप्त होता हो, तब $\frac{a}{b}$ से ज्ञात कीजिए।

View Solution

यदि $x = \frac{1}{z}$ तथा y= f(x), तो प्रदर्शित कीजिए कि $\frac{d^{2} f}{{d x}^{2}} = 2 z^{3} \frac{d y}{d z} + z^{4} \frac{d^{2} y}{{d z}^{2}}$

View Solution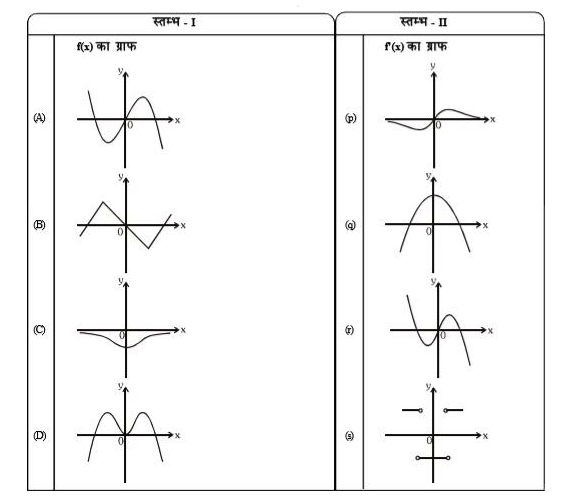

ocr_image

View Solution

माना $f (x) = {\begin{matrix} x & 0 < x \leq 2 के लिए 1 & x = 0 के लिए \end{matrix}$ ' है, तो x = 0 पर फलन का

View Solution

(a) सभी $x \in (0, 1)$ के लिए सत्य है -

View Solution

$L = lim x \to \infty {(\frac{log x}{x})}^{\frac{1}{x}}$

View Solution

Let $f (x) = \frac{{log}_{e} (x^{2} + e^{x})}{{log}_{e} (x^{4} + e^{2} x)}$ . If $lim x \to \infty f (x) = l$ and $lim x \to - \infty f (x) = m$ , then

View Solution

यदि $\int x^{5} e^{- x^{2}} d x = g (x) e^{- x^{2}} + c$ है, जहाँ c एक समाकलन अचर है तो $g (- 1)$ बराबर है

View Solution

एक फलन g जो प्रत्येक वास्तविक संख्या $x > 0$ के लिए परिभाषित है तथा $g (1) = 1, g' (x^{2}) = x^{3}$ को सभी $x > 0$ के लिए सन्तुष्ट करता है, तो g (4) का मान है

View Solution

$\frac{1}{(x + 3) (x + 4)}$ का आंशिक भिन्न रूप है-

View Solution

Let $f (0, \infty) \to (- \infty, \infty)$ be defined as $f (x) = e^{x} + ln x$ and $g = f^{- 1}$ , then find the $g' (e)$ .

View Solution

कॉलम I में दिये गये वक्तव्यों का कॉलम II में दिये अंतरालों अथवा अंतरालों के सम्मिलन से सुमेल करें
$\begin{matrix} कॉलम -I & कॉलम - II (A) & समुच्चय {R e (\frac{2 i z}{1 - z^{2}}) : z एकसम्मिश्र संख्या है | z | = 1, z \neq \pm 1} है & (p) (- \infty, - 1) \cup (1, \infty) (B) & फलन f (x) = {sin}^{- 1} (\frac{8 {(3)}^{x - 2}}{1 - 3^{2 (x - 1)}}) का प्रान्त है & (q) (- \infty, 0) \cup (0, \infty) (C) & यदि f (θ) = ∣ ∣ ∣ ∣ \begin{matrix} 1 & tan θ & 1 - tan θ & 1 & tan θ - 1 & - tan θ & 1 \end{matrix} ∣ ∣ ∣ ∣, तब समुच्चय {f (θ) : 0 \leq θ < \frac{π}{2}} है & (r) [2, \infty) (D) & यदि f (x) = x^{3 / 2} (3 x - 10), x \geq 0, तब f (x) किसमे वर्धमान है & (s) (- \infty, - 1] \cup [1, \infty) (t) (- \infty, 0] \cup [2, \infty) \end{matrix}$

View Solution

कॉलम I में दिये गये वक्तव्यों का कॉलम II में दिये अंतरालों अथवा अंतरालों के सम्मिलन से सुमेल करें
$\begin{matrix} कॉलम -I & कॉलम - II (A) & समुच्चय {R e (\frac{2 i z}{1 - z^{2}}) : z एकसम्मिश्र संख्या है | z | = 1, z \neq \pm 1} है & (p) (- \infty, - 1) \cup (1, \infty) (B) & फलन f (x) = {sin}^{- 1} (\frac{8 {(3)}^{x - 2}}{1 - 3^{2 (x - 1)}}) का प्रान्त है & (q) (- \infty, 0) \cup (0, \infty) (C) & यदि f (θ) = ∣ ∣ ∣ ∣ \begin{matrix} 1 & tan θ & 1 - tan θ & 1 & tan θ - 1 & - tan θ & 1 \end{matrix} ∣ ∣ ∣ ∣, तब समुच्चय {f (θ) : 0 \leq θ < \frac{π}{2}} है & (r) [2, \infty) (D) & यदि f (x) = x^{3 / 2} (3 x - 10), x \geq 0, तब f (x) किसमे वर्धमान है & (s) (- \infty, - 1] \cup [1, \infty) (t) (- \infty, 0] \cup [2, \infty) \end{matrix}$

View Solution

सीमायें जो अनिधार्य रूप $1^{\infty}, 0^{\circ}, \infty^{\circ}$ रखती है , को हल करने क लिए पहले लघुगणक लेते है , तब लॉपिटल नियम का उपयोग करते है।
माना $L = lim x \to a {(f (x))}^{g (x)}, \infty^{\circ}$ रूप में है , जिसे $e^{lim x \to a g (x) ln f (x)} = e^{L}$ की तरह लिखा सकते है , जहाँ $L = Lim x \to 1 \frac{ln f (x)}{1 / g (x)}, \frac{\infty}{\infty}$ रूप में है तथा लॉपिटल नियम द्वारा हल किया जा सकता है।
उपरोक्त जानकारी के आधार पर , निम्न प्रश्नों के उत्तर दीजिए :
$Lim x \to 1^{+} x^{1 / (1 - x)}$

View Solution

सीमायें जो अनिधार्य रूप $1^{\infty}, 0^{\circ}, \infty^{\circ}$ रखती है , को हल करने क लिए पहले लघुगणक लेते है , तब लॉपिटल नियम का उपयोग करते है।
माना $L = lim x \to a {(f (x))}^{g (x)}, \infty^{\circ}$ रूप में है , जिसे $e^{lim x \to a g (x) ln f (x)} = e^{L}$ की तरह लिखा सकते है , जहाँ $L = Lim x \to 1 \frac{ln f (x)}{1 / g (x)}, \frac{\infty}{\infty}$ रूप में है तथा लॉपिटल नियम द्वारा हल किया जा सकता है।
उपरोक्त जानकारी के आधार पर , निम्न प्रश्नों के उत्तर दीजिए :
$Lim x \to \infty [{(ln x)}^{1 / 2 x} + x^{1 / x^{n}}] \forall n \in N$ -

View Solution

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

ALLEN HINDI-METHODS OF DIFFERENTIATION-EXERCISE - 03 (MISCELLANEOUS TYPE QUESTIONS )(कथन एवं कारण )