निम्न प्रश्नों में दो कथन दिए गए है, एक को कथन - I तथा दूसरे को कथन - II के रूप में अंकित किया गया है।
(A) कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
(B) कथन- सत्य है, कथन-II सत्य है , कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
(C) कथन - I सत्य है परन्तु कथन - II असत्य है।
(D) कथन - I असत्य है परन्तु कथन - II सत्य है।
कथन-I : संख्या 1,21/2,31/3,41/4,51/5,61/6,71/7 में से सबसे बड़ी संख्या 31/3 है।
क्योंकि
कथन-II: x1/x,0<x<e के लिए वर्धमान तथा x>e के लिए ओसमान है।
A
B
C
D
The correct Answer is:A
Step by step video, text & image solution for निम्न प्रश्नों में दो कथन दिए गए है, एक को कथन - I तथा दूसरे को कथन - II के रूप में अंकित किया गया है। (A) कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है। (B) कथन- सत्य है, कथन-II सत्य है , कथन-II, कथन-I का सही स्पष्टीकरण नहीं है। (C) कथन - I सत्य है परन्तु कथन - II असत्य है। (D) कथन - I असत्य है परन्तु कथन - II सत्य है। कथन-I : संख्या 1,2^(1//2) , 3^(1//3) , 4^(1//4) , 5^(1//5), 6^(1//6), 7^(1//7) में से सबसे बड़ी संख्या 3^(1//3) है। क्योंकि कथन-II: x^(1//x) , 0 lt x lt e के लिए वर्धमान तथा x gt e के लिए ओसमान है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - MONOTONOCITYEXERCISE - EXERCISE - 03 MISCELLANEOUS TYPE QUESTIONS गद्यांश आधारित प्रश्न (Comprehension Based Questions)6videos
MONOTONOCITY
- BOOK - ALLEN HINDICHAPTER - MONOTONOCITYEXERCISE - EXERCISE - 04 [A] (CONCEPTUAL SUBJECTIVE EXERCISE)42videos
MONOTONOCITY
- BOOK - ALLEN HINDICHAPTER - MONOTONOCITYEXERCISE - EXERCISE - 03 MISCELLANEOUS TYPE QUESTIONS ( स्तम्भ सुमेलन (Match the column) )1videos
MONOTONOCITY
- BOOK - ALLEN HINDICHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - EXERCISE - 05 [B]12videos
METHODS OF DIFFERENTIATION
- BOOK - ALLEN HINDICHAPTER - PARABOLA EXERCISE - DO YOURSELF - 72videos
PARABOLA
Similar Questions
गद्यांश 1
माना f:(0,∞)→(−π2,π2),f(x)=arctan(lnx) से परिभाषित एक फलन है।
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नों के उत्तर दीजिए:
उपरोक्त फलन को निम्न में वर्गीकृत किया जा सकता है -02:00View Solutionनिम्न फलनों के लिए एकदिष्टता का अन्तराल ज्ञात कीजिए तथा अपने हलों के समुच्चय को संख्या रेखा पर प्रदर्शित कीजिए।
(a) f(x)=2.ex2−4x01:47View Solutionनिम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
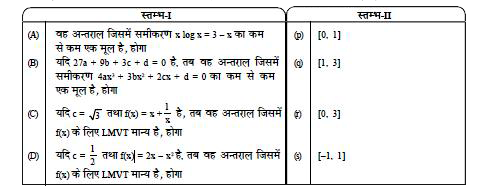
03:19View Solutionयदि ln (x+y) = 2xy हो , तो y'(0) =
03:21View Solutionरेखाओं x=4,y=4 तथा निर्देशी अक्षो से बने वर्गीय क्षेत्र को परवलय y2=4x तथा x2=4y विभाजित करते है। यदि S1,S2,S3 क्रमशः इन भागो के क्षेत्रफल ऊपर से नीचे की ओर अंकित है, तो S1:S2:S3 ज्ञात कीजिए।
View Solutionनिम्न कथन सत्य है या असत्य|
एक आव्यूह एक संख्या को निरूपित करता है ।View Solutionकथन सत्य है या असत्य
त्रिभुज कि भुजाओ के लम्ब समद्विभाजक संगामी होते है।View Solutionयदि z एक सम्मिश्र संख्या है, तो निम्न में से कौन-सा कथन सत्य है?
View Solutionनिम्न कथन सत्य है या असत्य-
Y -अक्ष के समान्तर समतल समीकरण ax+by+d=0 है।View Solutionनिम्नलिखित में से कौनसा कथन सही है ?
View Solutionनिम्नलिखित में से कौनसा कथन सही है?
View Solutionसही कथन है
View Solutionनिम्नलिखित में से कौनसा कथन सही है?
View Solutionदिए गए कथन में से कौन सा सही नहीं है?
View Solutionनिम्नलिखित में से कौन सा कथन सत्य है?
View Solutionनिम्नलिखित में से सही कथन है-
View Solution