If I1,I2,I3 are excentres of the triangle with vertices (0, 0), (5, 12), (16, 12) then the orthocentre of ΔI1I2I3 is Solution in Telugu
The correct Answer is:(7,9)
Step by step video, text & image solution for If I_(1), I_(2), I_(3) are excentres of the triangle with vertices (0, 0), (5, 12), (16, 12) then the orthocentre of DeltaI_(1)I_(2)I_(3) is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 2D-COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 2D-COORDINATE SYSTEMEXERCISE - EXERCISE -1.2 (VERY SHORT ANSWER QUESTIONS)
13 Videos
- 3D COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D COORDINATE SYSTEMEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II PRACTICE SHEET (ADVANCED)) (Integer Type Questions)
1 Videos
Similar Questions
Find the point which divides the line segment joining
(-1,2), (4,-5) in the ratio 3 : 2
View SolutionIf the circumcentre of the triangle whose vertices are (3, 2, -5), (-3, 8, -5) and (-3, 2, 1) is (−1,λ,−3) the integer λ must be equal to .
View SolutionI1=∫π20sinx−cosx1+sinxcosxdx,I2=∫2π0cos6xdx,I3=∫π2π2sin3xdx,I4=∫101n(1x−1)dx.Then I2=I3=I4=0,I1≠0 I1=I2=I3=0,I4≠0 I1=I2=I3=0,I4≠0 I1=I2=I3=0,I4≠0
View SolutionThe triangle formed by joining the three excentres I_(1),I_(2) and I_(3) of Delta ABC is called the excentral orexcentrictriangle and in this case interal angle bisector of triangle ABC are the altitudes of triangles I_(1)I_(2)I_(3) Incentre I of Delta ABC is the ......... of the excentral Delta I_(1)I_(2)I_(3).
View SolutionIf I_(1),I_(2),I_(3) are excentres of the triangle with vertices (0,0),(5,12),(16,12) then the orthocentre of Delta I_(1)I_(2)I_(3) is
View SolutionFind relation in between current i_(1), i_(2), i_(3), i_(4), i_(5)" and "i_(6) .
View SolutionIf I1,I2,I3 are the centers of escribed circles of ΔABC, show that the area of ΔI1I2I3 is (abc)/(2r)
View SolutionIf In=∫π/40tannxdx, then
1I2+I4,1I3+I5,1I4+I6,... from\
View SolutionIf I_(n)=int_(0)^(pi)(1-sin2nx)/(1-cos2x)dx then I_(1),I_(2),I_(3),"….." are in
View SolutionΔI1I2I3 is an excentral triangle of an equilateral triangle ΔABC such that I1I2=4 unit, if ΔDEF is pedal triangle of ΔABC, then Ar(ΔI1I2I3)Ar(ΔDEF)=
View SolutionIf I1,I2,I3 are excentres of the triangle with vertices (0, 0), (5, 12), (16, 12) then the orthocentre of ΔI1I2I3 is
View SolutionI,I1,I2,I3 are the in centre and excentres of ΔABC .If I(0,0),I1(2,3),I2(5,7) then the, distance between the orthocentres of ΔII1I3 and ΔI1I2I3is
View SolutionIf In=∫cotnxdx then I0+I1+2(I2+I3)+I4+I5=
View SolutionLet O be the circumcentre, H be the orthocentre, I be the incentre and I1I2,I3 be the excentres of acuteangled ΔABC
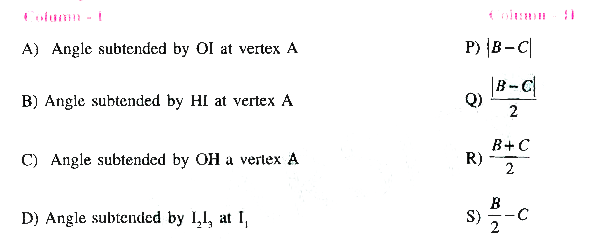
View SolutionIf I_(n)=int_(0)^(pi)(1-sin2nx)/(1-cos2x)dx then I_(1),I_(2),I_(3),"….." are in
View SolutionΔI1I2I3 is an excentral triangle of an equilateral triangle ΔABC such that I1I2=4 unit, if ΔDEF is pedal triangle of ΔABC, then Ar(ΔI1I2I3)Ar(ΔDEF)=
View Solution
