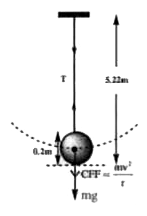
A sphere of radius 0.1 m and mass 8π kg is attached to the lower end of a steel wire of length 5.0 m and diameter 10−3m. The wire is suspended from 5.22 m high ceiling of a room. When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position. Y for steel =1.994×1011N/m2.
 Solution in Telugu
Solution in Telugu
As the length of the wire is 5m and diameter 2×0.1=0.2m and at lowest point it grazes the floor which is at a distance 5.22 m from the roof, the increase in length of the wire at lowest point
ΔL=5.22−(5+0.2)=0.02m
So tension in the wire (due to elasticity)
T=YALΔL
=1.994×1011×π(5×10−4)2×0.025=199.4πN
and as equation of circular motion of a mass .m. tied to a string in a vertical plane is (mv2/r)=T−mgcosθ
So at lowest point (mv2/r)=T−mg [asθ=0]
But her r=5+0.02+0.1=5.12m
So, (8πv2/5.12)=(1.99.4π−8π×9.8)
i.e., v2=(121×5.12/8)=77.44, so v=8.8m/s.
Similar Questions
A steel wire of length 5 m and diameter 10−3 m is hanged vertically from a ceiling of 5.22 m height. A sphere of radius 0.1 m and mass 8tt kg is tied to the free end of the wire. When this sphere is oscillated like a simple pendulum, it touches the floor of the room in its velocity of the sphere in its lower most position. Calculate the velocity of the sphere in its lower Young's modulus for in its lower most position. Young's modulus for steel =1.994×1011Nm−2.
View SolutionA sphere of radius 0.1m and mass 8 pi kg is attached to the lower end of a steel wire of length 5.0 m and diameter 10^(-3) . The wire is suspended from 5.22 m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994xx10^(11) N//m^(2)) .
View SolutionA sphere of radius 10cm and mass 25 kg is attached to the lower end of a steel wire of length 5m and diameter 4mm which is suspended from the ceiling of a room . The point of support is 521cm above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position (Ysteel=2×1011N/m2).
View SolutionA sphere of radius 0.1m and mass 8pikg is attached to the lower end of a steel wire of length 5.0m and diameter 10^(-3)m . The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lower point. Calculate the velocity of the sphere at the lowest position . Y for steel =1.994xx10^(11)N//m^(2) .
View SolutionA sphere of radius 0.10 m and mass 25 kg is attached to the lower end of a steel wire and the wire is suspended from the ceiling of the room and the base point is from the floor. 5.21 m is up. When the sphere is swinging like a simple pendulum, its lower point just touches the floor. Find the velocity of the sphere at the lowest point. Young's Coefficient of Steel 2 xx 10^(11) "न्यूटन/मी"^(2) Unstretched length of wire is 5.00 m and radius of steel wire 5 xx 10 ^(-4) I am
View Solution0.1 m radius and 8pikg A sphere of mass, 5.0 m, length 10^(-3)m is attached to the lower end of a steel wire of dia. The wire is suspended from a 5.22 m high ceiling of a room. When the sphere is oscillated like a simple pendulum, it touches the surface exactly at its lowest point. Touches the page exactly at the lowest position point. Calculate the velocity of the sphere at the lowest position. for steel Y=1.994xx10^(11)Nm^(-2)
View SolutionA sphere of radius 0.1 m and mass 8π kg is attached to the lower end of a steel wire of lengh 5.0m and diameter 10−3. The wire is suspended from 5.22 m high ceiling of a room. When the sphere is made to swint as a simple pendulum, it just grazes the floor at its lower point. Calculate the velocity of the sphere at the lowest position. Y for steel = 1.994×1011N/m2.
View Solution
