माना इकाई का एक सम्मिश्र घनमूल है, जहाँ . एक निष्पक्ष पाँसा तीन बार उछाला जाता है। यदि एवं पाँसे के उछाले जाने पर प्राप्त अंक दर्शाते हैं, तो की प्रायिकता निम्न है
The correct Answer is:C
Step by step video, text & image solution for माना omega इकाई का एक सम्मिश्र घनमूल है, जहाँ omega != 1. एक निष्पक्ष पाँसा तीन बार उछाला जाता है। यदि r_(1), r_(2) एवं r_(3) पाँसे के उछाले जाने पर प्राप्त अंक दर्शाते हैं, तो omega^(r_(1)) +omega^(r_(2)) + omega^(r_(3)) = 0 की प्रायिकता निम्न है by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBOOK - ALLEN HINDICHAPTER - PROBABILITYEXERCISE - Exercise-05 [A] JEE-[MAIN] Previous Year Questions
22 Videos
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -05 [B] (JEE ADVANCED : PREVIOUS YEAR QUESTIONS)
29 Videos
- क्रमचय तथा संचय BOOK - ALLEN HINDICHAPTER - क्रमचय तथा संचय EXERCISE - EXERCISE -04 [B]
14 Videos
Similar Questions
तीन छात्रों व्दारा एक प्रश्न हल करने की प्रायिकताएँ क्रमशः 12,13,14 है । प्रश्न के हल हो जाने की प्रायिकता हैं -
View Solution(a) उस समतल का समीकरण ज्ञात कीजिए जो बिन्दुओं (2,1,0),(5,0,1) और (4,1,1) से गुजरता हो। (b) यदि बिन्दु P(2, 1, 6) है, तो बिन्दु Q ज्ञात कीजिए ताकि PQ, समतल (a) के लम्बवत् हो तथा PQ का मध्य बिन्दु उस पर स्थित हो।
View Solution7 भिन्न रंगों में काउंटर उपलब्ध हैं। रंग को छोड़कर सभी का काउंटर समान है तथा प्रत्येक रंग के कम से कम 7 काउंटर है। कितने प्रकार से 10 काउंटरों को व्यवस्थित किया जा सकता है ? इनमे से कितनी व्यवस्थाओं में प्रत्येक रंग के काउंटर होंगे ?
View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
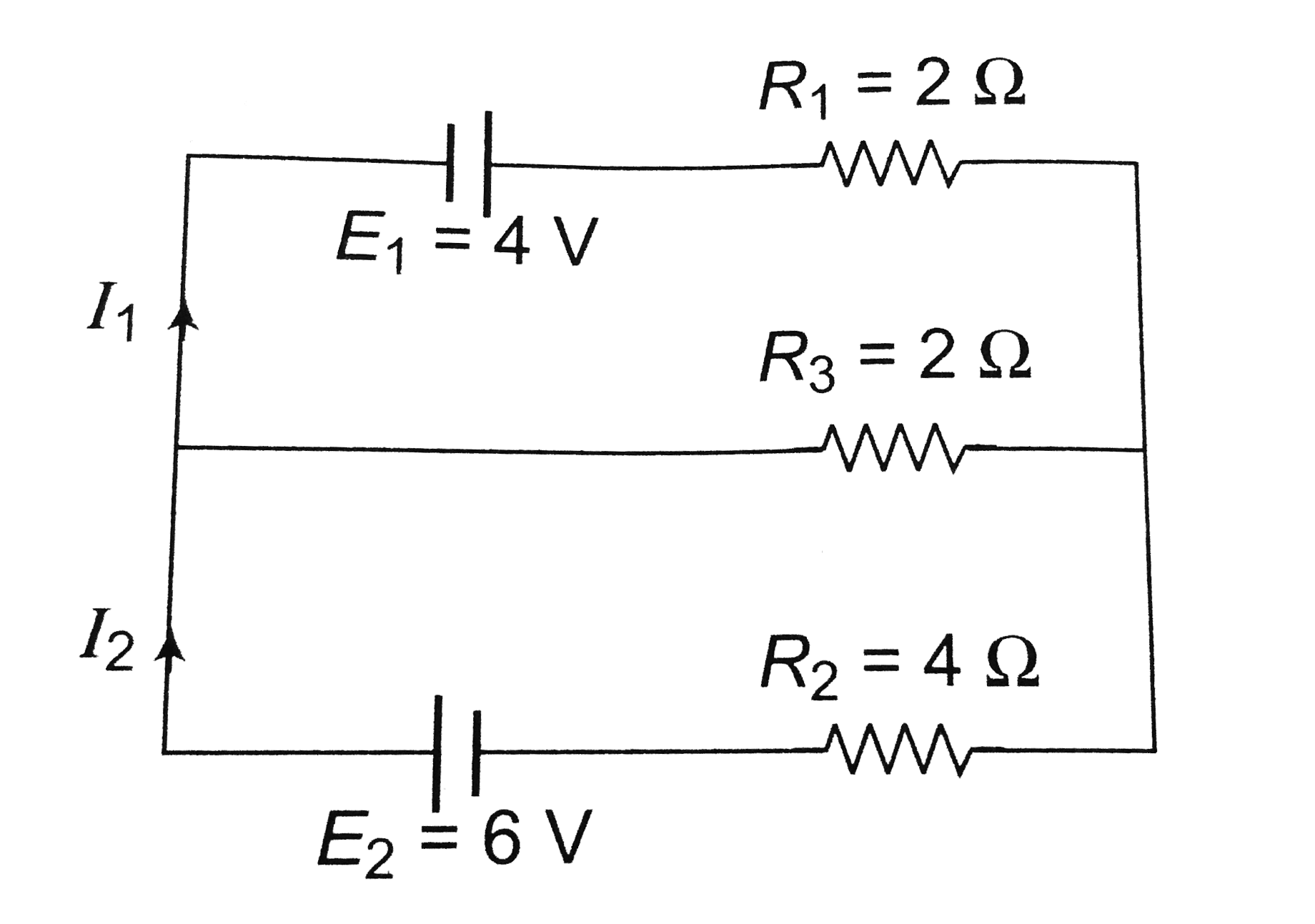
View SolutionIn the circuit shown in the figure R_(1) =3 Omega,R_(2) = 2 Omega and R_(3) = 5 Omega Emf of the cell epsilon = 6 Volt. (a) Infinitely many 1 Omega resistors are added in parallel to R_(1) and R_(2) . Find current through R_(2) and potential drop across it. (b) Infinitely many 1 Omega resistors are added in series to R_(3) . Find the potential drop across R_(3) and current through it.
View Solutionमाना कि ω इकाई का एक सम्मिश्र घनमूल है जहाँ ω≠ है। एक निष्पक्ष पाँसा तीन बार उछाला जाता है। यदि r1,r2 और r3 पाँसे के उछाले जाने पर प्राप्त अंक दर्शाते है तो ωr1+ωr2+ωr3=0 होने की प्रायिकता है-
View SolutionTwo dices are rolled and numbers r1 and r2 are chosen. Let 1+ωr1+ωr2=λ (where ω is a complex cube root of unity). Then
View Solutionयदि ω इकाई का एक घनमूल हो, तो सारणिक ∣∣ ∣ ∣∣1ω4ω8ω4ω81ω81ω4∣∣ ∣ ∣∣ का मान है-
View Solutionमाना ω एक सम्मिश्र संख्या ऐसी है कि 2ω+1=z जहाँ, z=√−3 है। यदि ∣∣ ∣ ∣∣1111−ω2−1ω21ω2ω2∣∣ ∣ ∣∣=3k है तो k बराबर है
View SolutionIf the charge on the capacitor is 1 mC in the given circuit, then (R_(1)R_(2))/(R_(3))= . . . . . Omega .
View SolutionLet ω be a complex cube a root of unity with ω≠1 . A fair die is thrown three times . If r1,r2andr3 are the numbers obtained on the die , then the probability that ωr1+ωr2+ωr3=0 is :
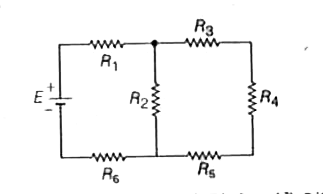
View Solutionचित्र में दिखाई गई बैटरी से निकली धारा का मान (ऐम्पियर में) क्या होगा? दिया गया है,
R1=15Ω,R2=10Ω,R3=20Ω,R4=5Ω.R5=25Ω,R6=30Ω, E = 15 V
View Solutionमाना ω इकाई का एक सम्मिश्र घनमूल है, जहाँ ω≠1. एक निष्पक्ष पाँसा तीन बार उछाला जाता है। यदि r1,r2 एवं r3 पाँसे के उछाले जाने पर प्राप्त अंक दर्शाते हैं, तो ωr1+ωr2+ωr3=0 की प्रायिकता निम्न है
View SolutionThe measurement of an unknown resistance R is to be carried out using Wheatstone bridge as given in the figure below. Two students perform an experiment in two ways. The first students takes R_(2) = 10 Omega and R_(1) = 5 Omega . The other student takes R_(2) = 1000 Omega and R_(1) = 500 Omega . In the standard arm, both take R_(3) = 5 Omega . both find R = (R_(2))/(R_(1)) , R_(3) = 10 Omega within errors.
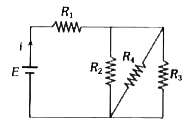
View Solutionदिखाये गये परिपथ में E=6.0V,R1=100Ω,R2=R3=50Ω,R4=75Ω है। परिपथ का तुल्य प्रतिरोध, Ω में होगा
View Solutionमाना कि ω, इकाई का एक सम्मिश्र धनमूल हैं जहां ω≠1 एक निष्पक्ष पांसा तीन बार उछाला जाता है। यदि r1,r2 एवं r2 पांसे के उछाले जाने पर प्राप्त अंक दर्शाते है तो ωr1+ωr2+ωr3=0 होने की प्रायिकता निम्न है
View Solution
