माना S1, समीकरण (1+a)cosθcos(2θ−b)=(1+acos2θ)cos(θ−b) के सभी हलों का समुच्चय है, जो a व b से स्वतंत्र है तथा S2 उन सभी हलों का समुच्चय है जो a व b पर आश्रित है।
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नों के उत्तर दीजिए:
यदि a = 0 तथा S2,(0,π) का उप समुच्चय है, तब b के सभी संभव मान है -
b∈(−nπ,2nπ),n∈Z
b∈(−nπ,2π−nπ),n∈Z
b∈(−nπ,nπ),n∈Z
इनमें से कोई नहीं
The correct Answer is:B
Step by step video, text & image solution for माना S_(1), समीकरण (1+a)cos theta cos(2theta-b)=(1+acos2theta)cos(theta-b) के सभी हलों का समुच्चय है, जो a व b से स्वतंत्र है तथा S_(2) उन सभी हलों का समुच्चय है जो a व b पर आश्रित है। उपरोक्त जानकारी के आधार पर, निम्न प्रश्नों के उत्तर दीजिए: यदि a = 0 तथा S_(2), (0, pi) का उप समुच्चय है, तब b के सभी संभव मान है - by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमीतीय समीकरणBook:ALLEN HINDIChapter:त्रिकोणमीतीय समीकरणExercise:EXERCISE-04 [A] CONCEPTUAL SUBJECTIVE EXERCISE
Explore 20 Videos
- त्रिकोणमीतीय समीकरणBook:ALLEN HINDIChapter:त्रिकोणमीतीय समीकरणExercise:EXERCISE-04 [B] BRAIN STORMING SUBJECTIVE EXERCISE
Explore 10 Videos
- त्रिकोणमीतीय समीकरणBook:ALLEN HINDIChapter:त्रिकोणमीतीय समीकरणExercise:EXERCISE-03 MISCELLANEOUS TYPE QUESTIONS (कथन एवं कारण)
Explore 2 Videos
- त्रिकोणमितीय अनुपात एवं सर्वसमिकायें Book:ALLEN HINDIChapter:त्रिकोणमितीय अनुपात एवं सर्वसमिकायें Exercise:EXERCISE - 04 [B] (BRAIN STORMING SUBJECTIVE EXERCISE)
Explore 11 Videos
- त्रिभुज के हल Book:ALLEN HINDIChapter:त्रिभुज के हल Exercise:DO YOURSELF 10
Explore 1 Video
Similar Questions
यदि sinA=sinB तथा cosA=cosB हो, तो A का मान B के पदों में ज्ञात कींजिए।
View Solutionसमीकरण से θ के व्यापक मान ज्ञात कीजिए -
cosθ⋅cos2θ⋅cos3θ=14
View Solutionकथन-I : θ≠(2n+1)π या (2n+1)π/2,n∈I के किसी वास्तविक मान के लिए व्यंजक y=cos2θ−1cos2θ+cosθ का मान y≤0 या y≥2
क्योंकि
कथन-II : θ के सभी वास्तविक मानों के लिए secθ∈(−∞,−1]∪[1,∞)
View Solutionसिद्ध कीजिए:
न्यूनकोण त्रिभुज ABC में ΣsecA तथा Σtan2A का न्यूनतम मान क्रमश: 6 तथा 9 है।
View Solutionएक समबाहु त्रिभुज में, सिद्ध कीजिए कि केन्द्रक और परिवृत्त का केन्द्र (परिकेन्द्र) सम्पाती होते हैं |
View Solutionमाना a,b,c वास्तविक संख्याएं है। माना x,y,z ऐसी वास्तविक संख्या है जो कभी शून्य नहीं हैं तथा x=cy+bz,y=az+cx तथा z=bx+ay, तो a2+b2+c2+2abc का मान है:
View Solutionएक द्विआधारी संक्रिया ∗Z+ पर निम्न रूप परिभाषित है :
a∗b=ab−bजहाँa,b∈Z+
2∗5 का मान ज्ञात कीजिए , जहाँ Z+ धनात्मक पूर्णांकों का समुच्चय है ।
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न के रेखीय कार्य योजना का सम्भाव्य क्षेत्र के निम्न प्रकार का है:
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।
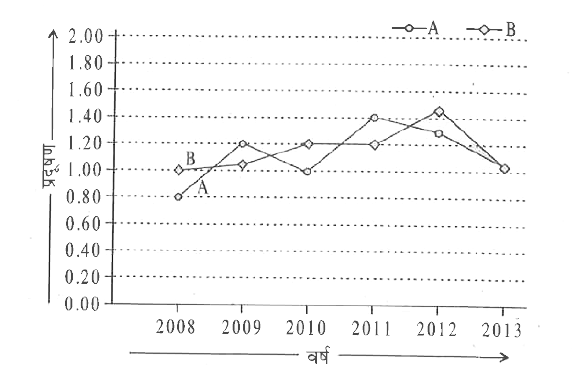
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
दिये गये वर्षो में से कितने वर्षो में B का प्रदूषण A के प्रदूषण से कम रहा है ?
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
दिये गये वर्षो में से कितने वर्षो में B का प्रदूषण A के प्रदूषण से कम रहा है ?

View Solutionसमीकरण निकाय x+y=2π3,cosx+cosy=32, जहाँ x और y वास्तविक है , के हलों का समुच्चय ………….. है।
View Solutionउस सरल रेखा का समीकरण जो बिन्दु (1,-2) से गुजरती है तथा रेखा 3x-5y+7=0 के लम्बवत है, है
View Solutionउस सरल रेखा का समीकरण जो रेखाओं 3x-y+ 2 = 0 तथा 5x-2y+ 7 = 0 के प्रतिच्छेद बिन्दु से गुजरती है तथा जिसकी प्रवणता अनन्त है, होगा
View Solution

