The value of √i is
1-i
1+i
±(1+i)
±1√2(1+i)
The correct Answer is:D
To find the value of √i, we can follow these steps:
Step 1: Express i in polar form
The complex number i can be represented in polar form. We know that:
i=0+1i
In polar form, this can be expressed as:
i=r⋅eiθ
where r is the modulus and θ is the argument (angle).
Step 2: Calculate the modulus r
The modulus r of i is given by:
r=|i|=√02+12=√1=1
Step 3: Determine the argument θ
The argument θ for i is:
θ=π2(since it lies on the positive imaginary axis)
Step 4: Write i in polar form
Now we can write i in polar form:
i=1⋅eiπ2
Step 5: Find the square root of i
To find √i, we take the square root of the polar form:
√i=√1⋅eiπ2=√1⋅eiπ4=1⋅eiπ4=eiπ4
Step 6: Convert back to rectangular form
Now we convert eiπ4 back to rectangular form:
eiπ4=cos(π4)+isin(π4)=1√2+i1√2
Step 7: Include the negative root
Since we are looking for both roots, we also consider the negative:
√i=±(1√2+i1√2)
Final Answer
Thus, the value of √i is:
√i=±(1√2+i1√2)
---
The complex number i can be represented in polar form. We know that:
i=0+1i
In polar form, this can be expressed as:
i=r⋅eiθ
where r is the modulus and θ is the argument (angle).
The modulus r of i is given by:
r=|i|=√02+12=√1=1
The argument θ for i is:
θ=π2(since it lies on the positive imaginary axis)
Now we can write i in polar form:
i=1⋅eiπ2
To find √i, we take the square root of the polar form:
√i=√1⋅eiπ2=√1⋅eiπ4=1⋅eiπ4=eiπ4
Now we convert eiπ4 back to rectangular form:
eiπ4=cos(π4)+isin(π4)=1√2+i1√2
Since we are looking for both roots, we also consider the negative:
√i=±(1√2+i1√2)
Thus, the value of √i is:
√i=±(1√2+i1√2)
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - A DAS GUPTACHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
224 Videos
- Circular Functions, Identities BOOK - A DAS GUPTACHAPTER - Circular Functions, Identities EXERCISE - Exercise
300 Videos
- Continuity, Differentiability and Graph of FunctionBOOK - A DAS GUPTACHAPTER - Continuity, Differentiability and Graph of FunctionEXERCISE - Exercise
38 Videos
Similar Questions
The value of
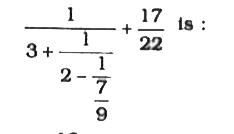 is.
is.
View SolutionThree prizes are to distributed in a quiz contest. The value of the first prize is 32 of the value of the second and the value of the third prize is five sixth the value of the second prize. If total value of the 3 prizes is Rs.800, find the value of each prize.
View Solution
Knowledge Check
The value of

 is-A5994B51003C2994D3994
is-A5994B51003C2994D3994The value of √i+√−i is :
A1B√2C-iDnone of theseIf in general , the value of sin A is known , but the value of A is not known , then how many values of tan (A2) can be calculated ?
A1B2C3D4
The value of MPC is double the value of MPS. Find the value of multiplier.
View SolutionIn a transistor, the value of β is 50. Calculate the value of α
View SolutionIn a transistor, the value of β is 60 Calculate the value of α .
View SolutionThree prizes are to be distributed in a quiz contest. The value of the second prize is five sixths the value of the first prize and the value of the third prize is four-fifths that of the second prize. If the total value of three prizes is Rs 150, find the value of each prize.
View SolutionIf the value of resistance is 10.845 ohm and the value of current is 3.23 amp, the value of potential with significant numbers would be
View Solution