A wire 88cm long bent into a circular loop is placed perpendicular to the magnetic field of density 2.5 Wb m−2. Within 0.5 s the loop is changed into square of each side 22 cm and the density is increased to 3Wbm−2. Calculate the value of e.m.f. induced.Solution in Punjabi
Step by step video & image solution for A wire 88cm long bent into a circular loop is placed perpendicular to the magnetic field of density 2.5 Wb m^(-2). Within 0.5 s the loop is changed into square of each side 22 cm and the density is increased to 3Wbm-2. Calculate the value of e.m.f. induced. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
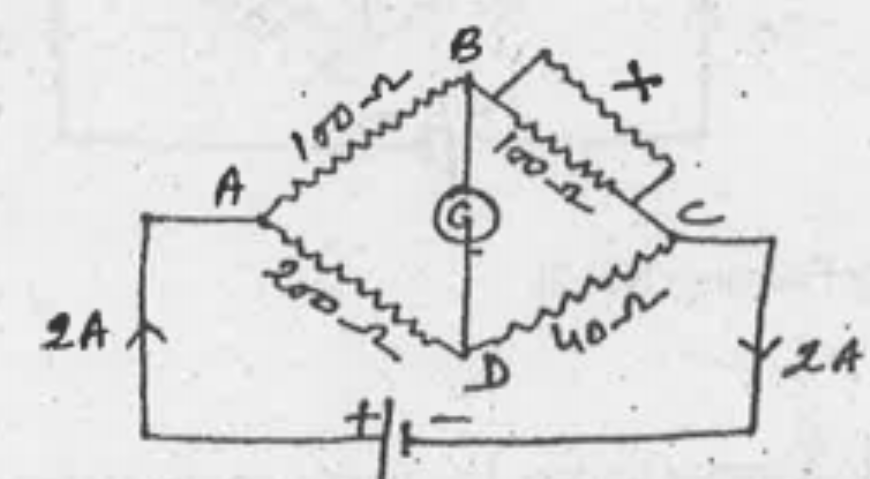
The given Wheatstone Bridge shows no deflection in the galvanometer joined between the points B and D.Calculate the value of ‘X’.
View SolutionFind the wavelengthof electromagnetic waves of frequencies 4×1017Hz in free space. Write its two applications.
View SolutionThe magnetic field through a circular loop of wire 12 cm in radius and 8.5 ohm resistance, changes with time as shown in Fig. The magnetic field is perpendicular to the plane of the loop. Calculate the induced current in the loop and plot is as a function of time.
View SolutionA wire 88 cm long bent into a circular loop is placed perpendicular to the magnetic field of flux density 2.5Wbm−2 . Whitin 0.5 sec, the loop is changed into a square of each side 22 am and flux density is increased to 3.0Wbm−2. Calculate the value of e.m.f.induced.
View SolutionA wire 88 cm long bent into a circular loop is placed perpendicular to the magnetic field of flux density is increased to 3.0 wbm−2. Calculate the value of the emf induced .
View SolutionA wire 40 cm long bent into a rectangular loop 15cm×5cm is placed perpendicular to the magnetic field whose flux density is 0.8Wbm−2. Within 1.0 second, the loop is changed into a 10 cm square and flux density increases to 1.4 Wbm−2. Calculate the value of induced emf.
View SolutionA square wire loop with sides 0.5 m is placed with its plane perpendicular to the magnetic field. The resistance of the loop is 5Ω. The rate at which the magnetic induction should be changed so that a current of 0.1 A is induced in the loop is
View SolutionA given wire is bent into a circular loop of radius 7cm and is placed perpendicular to a magnetic field of 1.0T.Within 0.1 second ,the loop is changed to a 100cm square and the field increases to 1.8T .The induced emf in the coil will be
View Solutionएक 88 cm लम्बा तार एक वृत्तीय लूप के रूपं में मोड़कर (folded) 2.5Wbm−2 फ्लक्स घनत्वं वाले चुम्बकीय क्षेत्र के लम्बवत् रखा गया है। 0.5 s में लूप को 22 cm भुजा वाले वर्ग की आकृति में बदल दिया जाता है और फ्लक्स घनत्व बढ़ाकर 3.0 Wbm−2 कर दिया जाता है । प्रेरित वि. वा. बल का मान ज्ञात कीजिए।
View Solution15cm × 5 cm के आयताकार लूप में मोड़ी गई एक 40 cm लम्बी तार, 0.8 Wb/m2 फ्लक्स घनत्व के चुम्बकीय क्षेत्र पर लम्बवत रखी जाती है। 0.5 s के अन्दर लूप, 10 cm के वर्ग में बदल जाता है और फलक्स घनत्व बढ़कर 1.4 Wb/m2 हो जाता है। प्रेरित विद्युत वाहक बल का मान वोल्ट में निकालें।
View Solution22 cm भुजा के वर्गाकार लूप को 0.4s में वृत्तीय लूप में परिवर्तित किया जाता है | 0.2T का समरूप चुम्बकीय क्षेत्र लूप में अभिलम्बवत हो तब लूप में प्रेरित वि वा बल होगा
View SolutionA wire loop is rotated in a magnetic field. The frequency of change of direction of the induced e.m.f is
View SolutionA given wire is bent into a rectangular loop of size 15cm×5cm and placed perpendicular to a magnetic field of 1.0 Tesla. Within 0.5sec, the loop is changed into a 10cm square and the field increases to 1.4 Tesla.Calculate the value of e.m.f. induced in the loop?
View SolutionA conducting loop in the form of a circule is placed in a uniform magnetic field with its place perpendicular to the direction of the field. An e.m.f. will be induced in the loop if
View SolutionA wire 88 cm long bent into a circular loop is kept with plane of the coil perpendicular to the magnetic induction 2.5 Wb//m^2 . Within 0.5 second, the coil is changed to a square and magnetic induction is increased by 0.5 Wb//m^2 . Calculate the e.m.f. induced in the wire.
View Solution

