The solubility product of aluminium sulphate is given by the expression
The correct Answer is:D
To find the solubility product (Ksp) of aluminium sulphate (Al₂(SO₄)₃), we can follow these steps:
Step 1: Write the Dissociation Equation
Aluminium sulphate dissociates in water according to the following equation:
Al2(SO4)3(s)⇌2Al3+(aq)+3SO2−4(aq)
Step 2: Define Initial Concentrations
Assume the initial concentration of aluminium sulphate is 1 M. At the start (before dissociation), we have:
- (Al³⁺) = 0 M
- (SO₄²⁻) = 0 M
Step 3: Define Change in Concentrations
Let the solubility of aluminium sulphate be s. As it dissociates, the changes in concentration will be:
- (Al³⁺) will increase by 2s (since 2 moles of Al³⁺ are produced for every mole of Al₂(SO₄)₃)
- (SO₄²⁻) will increase by 3s (since 3 moles of SO₄²⁻ are produced for every mole of Al₂(SO₄)₃)
At equilibrium, the concentrations will be:
- (Al³⁺) = 2s
- (SO₄²⁻) = 3s
Step 4: Write the Expression for Ksp
The solubility product (Ksp) is given by the expression:
Ksp=(Al3+)2⋅(SO2−4)3
Substituting the equilibrium concentrations into the Ksp expression:
Ksp=(2s)2⋅(3s)3
Step 5: Simplify the Expression
Now, simplify the expression:
Ksp=(22⋅s2)⋅(33⋅s3)
Ksp=4s2⋅27s3
Ksp=108s5
Final Result
Thus, the solubility product of aluminium sulphate is:
Ksp=108s5
Aluminium sulphate dissociates in water according to the following equation:
Assume the initial concentration of aluminium sulphate is 1 M. At the start (before dissociation), we have:
- (SO₄²⁻) = 0 M
Let the solubility of aluminium sulphate be s. As it dissociates, the changes in concentration will be:
- (SO₄²⁻) will increase by 3s (since 3 moles of SO₄²⁻ are produced for every mole of Al₂(SO₄)₃)
- (SO₄²⁻) = 3s
The solubility product (Ksp) is given by the expression:
Now, simplify the expression:
Ksp=4s2⋅27s3
Ksp=108s5
Thus, the solubility product of aluminium sulphate is:
Topper's Solved these Questions
- PRACTICE PAPER 1Book:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPER 1Exercise:Practice Paper 1
Explore 44 Videos
- ORGANIC CHEMISTRY-SOME BASIC PRINCIPLES AND TECHNIQUES Book:NCERT FINGERTPS ENGLISHChapter:ORGANIC CHEMISTRY-SOME BASIC PRINCIPLES AND TECHNIQUES Exercise:Assertion And Reason
Explore 12 Videos
- PRACTICE PAPER 2Book:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPER 2Exercise:Practice Paper 2
Explore 44 Videos
Similar Questions
Knowledge Check
solubility product of radium sulphate is 4×10−9. What will be the solubility of Ra2+ in 0.10M NaSO4?
A4×10−10MB2×10−5MC4×10−5MD2×10−10M
The solubility product of barium sulphate is 1.5×10−9 at 18∘C . Its solubility in water at 18∘C is
View SolutionThe solubility product of three sparingly soluble salts are given below:
(No,Formula,Solubility product),(1,PQ,4.0×10−20,(2,PQ2,3.2×10−14),(3,PQ3,2.7×10−35)
The correct order of decreasing molar solubility is
View SolutionThe solubility product of Hg2I2 is equal to
View SolutionAn aqueous solution of aluminium sulphate would show
View SolutionThe correct order of the solubility of alkaline- earth metal sulphates in water is :
View SolutionThe solubility product (Ksp) of the following compound are given at 25∘C
The most soluble and least soluble compound are :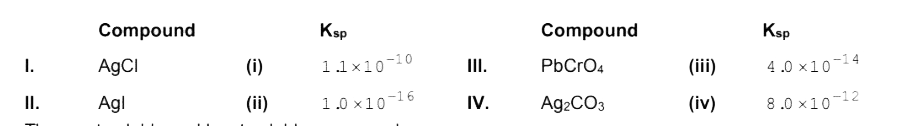
View SolutionSolubility of the alkaline earth's metal sulphates in water decreases in the sequence
View Solution

