NaBH4+I2→X+Y+Z
BF3+NaH450K−−→X+P
BF3+LiAIH4→X+Q+R
X,Y,Z,P,Q and R reaction are
XYZPQR
Na4B4O7NaIHIHFLiFAIF3
B2H6NaIH2NaFLiFAIF2
B2H6BH3NaIB3N3H6AI2F6AIF3
BH3,B2H6,H2,B3N3H6,LiF,AIF3
The correct Answer is:B
To solve the given reactions step by step, we will analyze each reaction and identify the products (X, Y, Z, P, Q, and R).
Step 1: Reaction of NaBH₄ with I₂
The reaction is:
NaBH4+I2→X+Y+Z
Products:
- When sodium borohydride (NaBH₄) reacts with iodine (I₂), it produces diborane (B₂H₆), sodium iodide (NaI), and hydrogen gas (H₂).
- The balanced equation is:
2NaBH4+I2→B2H6+2NaI+H2
Thus, we can identify:
- X = B₂H₆
- Y = NaI
- Z = H₂
Step 2: Reaction of BF₃ with NaH
The reaction is:
BF3+NaH450K→X+P
Products:
- When boron trifluoride (BF₃) reacts with sodium hydride (NaH), it produces diborane (B₂H₆) and sodium fluoride (NaF).
- The balanced equation is:
2BF3+6NaH→B2H6+6NaF
Thus, we can identify:
- X = B₂H₆
- P = NaF
Step 3: Reaction of BF₃ with LiAlH₄
The reaction is:
BF3+LiAlH4→X+Q+R
Products:
- When boron trifluoride (BF₃) reacts with lithium aluminum hydride (LiAlH₄), it produces diborane (B₂H₆), lithium fluoride (LiF), and aluminum fluoride (AlF₃).
- The balanced equation is:
3BF3+4LiAlH4→B2H6+3LiF+AlF3
Thus, we can identify:
- X = B₂H₆
- Q = LiF
- R = AlF₃
Summary of Products:
- X = B₂H₆
- Y = NaI
- Z = H₂
- P = NaF
- Q = LiF
- R = AlF₃
Final Answer:
The products are:
- X=B2H6
- Y=NaI
- Z=H2
- P=NaF
- Q=LiF
- R=AlF3
The reaction is:
NaBH4+I2→X+Y+Z
- When sodium borohydride (NaBH₄) reacts with iodine (I₂), it produces diborane (B₂H₆), sodium iodide (NaI), and hydrogen gas (H₂).
- The balanced equation is:
2NaBH4+I2→B2H6+2NaI+H2
- X = B₂H₆
- Y = NaI
- Z = H₂
The reaction is:
BF3+NaH450K→X+P
- When boron trifluoride (BF₃) reacts with sodium hydride (NaH), it produces diborane (B₂H₆) and sodium fluoride (NaF).
- The balanced equation is:
2BF3+6NaH→B2H6+6NaF
- X = B₂H₆
- P = NaF
The reaction is:
BF3+LiAlH4→X+Q+R
- When boron trifluoride (BF₃) reacts with lithium aluminum hydride (LiAlH₄), it produces diborane (B₂H₆), lithium fluoride (LiF), and aluminum fluoride (AlF₃).
- The balanced equation is:
3BF3+4LiAlH4→B2H6+3LiF+AlF3
- X = B₂H₆
- Q = LiF
- R = AlF₃
- X = B₂H₆
- Y = NaI
- Z = H₂
- P = NaF
- Q = LiF
- R = AlF₃
The products are:
- X=B2H6
- Y=NaI
- Z=H2
- P=NaF
- Q=LiF
- R=AlF3
Topper's Solved these Questions
- THE P-BLOCK ELEMENTSBook:NCERT FINGERTPS ENGLISHChapter:THE P-BLOCK ELEMENTSExercise:HIGHER ORDER THINKING SKILLS
Explore 9 Videos
- THE P-BLOCK ELEMENTSBook:NCERT FINGERTPS ENGLISHChapter:THE P-BLOCK ELEMENTSExercise:EXEMPLAR PROBLEMS
Explore 15 Videos
- STRUCTURE OF ATOM Book:NCERT FINGERTPS ENGLISHChapter:STRUCTURE OF ATOM Exercise:Assertion And Reason
Explore 15 Videos
- THE S-BLOCK ELEMENTSBook:NCERT FINGERTPS ENGLISHChapter:THE S-BLOCK ELEMENTSExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Knowledge Check
In Figure 1, y=√3xandz=2x. What is the ratio p:q:r in figure 2?
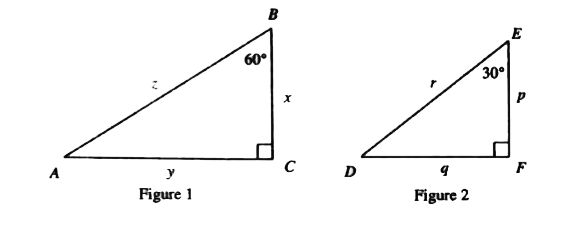 A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
If A = {x, y, z}, then the relation
R={(x,x),(y,y),(z,z),(z,x),(z,y)}, is
View SolutionMark six points P, Q, R, X, Y, Z such that P, Q,R are collinear and X,Y, Z are not collinear
View SolutionWrite the coefficient of:
(i)z in −7xyz
(ii) p in −3pqr
View SolutionIf the circles x2+y2+5Kx+2y+K=0 and 2x2+y2)+2Kx+3y−1=0,(K∈R) intersect at the point P and Q then the line 4x+5y−K=0 passes P and Q for :
View SolutionIn ΔABC and ΔPQR, AB=PQ, BC=QR and CB and RQ are extended to X and Y respectively and ∠ABX=∠PQY. Prove that ABC≅ PQR.
View SolutionIn the carbylamine reaction, R−X converted R−Y via the intermediate Z,R−X,R−YandZ, respectively are
View SolutionNormals of parabola y2=4x at P and Q meets at R(x2,0) and tangents at P and Q meets at T(x1,0). If x2=3, then find the area of quadrilateral PTQR.
View Solution

