What will be the amount of (NH4)2SO4 (in g) which must be added to 500 mL of 0.2 M NH4OH to yield a solution of pH 9.35? [Given,pKaof NH+4=9.26,pKbNH4OH=14−pKa(NH+4)]
a. 5.35
b. 6.47
c. 10.03
d. 7.34
The correct Answer is:A
To solve the problem of determining the amount of ammonium sulfate (NH4)2SO4 needed to achieve a pH of 9.35 in a 500 mL solution of 0.2 M ammonium hydroxide (NH4OH), we can follow these steps:
Step 1: Convert Volume to Liters
The volume of the solution is given as 500 mL. We need to convert this to liters:
Volume (L)=500 mL1000=0.5 L
Hint: Remember that 1 L = 1000 mL for conversion.
Step 2: Calculate Moles of Ammonium Hydroxide
Using the molarity and volume, we can calculate the number of moles of ammonium hydroxide:
Moles of NH4OH=Molarity×Volume=0.2M×0.5L=0.1moles
Hint: Moles can be calculated using the formula: Moles = Molarity × Volume.
Step 3: Determine pOH from pH
Since we are given the pH, we can find the pOH:
pOH=14−pH=14−9.35=4.65
Hint: The relationship between pH and pOH is given by the equation: pH + pOH = 14.
Step 4: Calculate pKb
Given that the pKa of the ammonium ion (NH+4) is 9.26, we can find pKb:
pKb=14−pKa=14−9.26=4.74
Hint: pKb can be found using the relationship between pKa and pKb.
Step 5: Use the Henderson-Hasselbalch Equation
Since we are dealing with a buffer solution, we can use the Henderson-Hasselbalch equation:
pOH=pKb+log((Salt)(Base))
Substituting the known values:
4.65=4.74+log((Salt)0.1)
Hint: The base in this case is the concentration of NH4OH.
Step 6: Rearranging the Equation
Rearranging the equation to solve for the ratio of salt to base:
log((Salt)0.1)=4.65−4.74=−0.09
Taking antilog:
(Salt)0.1=10−0.09≈0.8187
Thus,
(Salt)≈0.1×0.8187≈0.08187M
Hint: Remember that the antilogarithm can be calculated as 10value.
Step 7: Calculate Moles of Ammonium Ion
Since the salt is ammonium sulfate (NH4)2SO4, each mole of salt provides 2 moles of ammonium ions:
Moles of NH+4=0.08187M×0.5L=0.040935moles
Hint: Moles of ions can be calculated using the molarity of the salt and the volume of the solution.
Step 8: Calculate Moles of Ammonium Sulfate
Since each mole of ammonium sulfate produces 2 moles of ammonium ions:
Moles of (NH4)2SO4=0.0409352≈0.0204675moles
Hint: Divide the moles of ammonium ions by 2 to find the moles of ammonium sulfate.
Step 9: Calculate the Mass of Ammonium Sulfate
The molar mass of ammonium sulfate (NH4)2SO4 is calculated as follows:
- Nitrogen: 14×2=28
- Hydrogen: 1×4×2=8
- Sulfur: 32
- Oxygen: 16×4=64
Total molar mass:
28+8+32+64=132g/mol
Now, we can calculate the mass:
Mass=Moles×Molar Mass=0.0204675moles×132g/mol≈2.70g
Hint: Use the formula: Mass = Moles × Molar Mass to find the mass of the compound.
Final Answer
The amount of ammonium sulfate (NH4)2SO4 required is approximately 2.70 g.
The volume of the solution is given as 500 mL. We need to convert this to liters:
Volume (L)=500 mL1000=0.5 L
Using the molarity and volume, we can calculate the number of moles of ammonium hydroxide:
Moles of NH4OH=Molarity×Volume=0.2M×0.5L=0.1moles
Since we are given the pH, we can find the pOH:
pOH=14−pH=14−9.35=4.65
Given that the pKa of the ammonium ion (NH+4) is 9.26, we can find pKb:
pKb=14−pKa=14−9.26=4.74
Since we are dealing with a buffer solution, we can use the Henderson-Hasselbalch equation:
pOH=pKb+log((Salt)(Base))
Substituting the known values:
4.65=4.74+log((Salt)0.1)
Rearranging the equation to solve for the ratio of salt to base:
log((Salt)0.1)=4.65−4.74=−0.09
Taking antilog:
(Salt)0.1=10−0.09≈0.8187
Thus,
(Salt)≈0.1×0.8187≈0.08187M
Since the salt is ammonium sulfate (NH4)2SO4, each mole of salt provides 2 moles of ammonium ions:
Moles of NH+4=0.08187M×0.5L=0.040935moles
Since each mole of ammonium sulfate produces 2 moles of ammonium ions:
Moles of (NH4)2SO4=0.0409352≈0.0204675moles
The molar mass of ammonium sulfate (NH4)2SO4 is calculated as follows:
- Nitrogen: 14×2=28
- Hydrogen: 1×4×2=8
- Sulfur: 32
- Oxygen: 16×4=64
28+8+32+64=132g/mol
Mass=Moles×Molar Mass=0.0204675moles×132g/mol≈2.70g
The amount of ammonium sulfate (NH4)2SO4 required is approximately 2.70 g.
Topper's Solved these Questions
- EQUILIBRIUM Book:NCERT FINGERTPS ENGLISHChapter:EQUILIBRIUM Exercise:EXEMPLAR PROBLEMS
Explore 19 Videos
- EQUILIBRIUM Book:NCERT FINGERTPS ENGLISHChapter:EQUILIBRIUM Exercise:ASSERTION & REASON (CORNER)
Explore 15 Videos
- EQUILIBRIUM Book:NCERT FINGERTPS ENGLISHChapter:EQUILIBRIUM Exercise:Assertion And Reason
Explore 15 Videos
- ENVIRONMENTAL CHEMISTRYBook:NCERT FINGERTPS ENGLISHChapter:ENVIRONMENTAL CHEMISTRYExercise:Assertion And Reason
Explore 15 Videos
- HYDROCARBONS Book:NCERT FINGERTPS ENGLISHChapter:HYDROCARBONS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
To prepare a buffer of pH 8.26, amount of (NH4)2SO4 to be added into 500mL of 0.01MNH4OH solution [pKa(NH+4)=9.26] is:
View SolutionWhen NH4Cl is added to a solution of NH4OH:
View Solution20mL of 0.1M(H2SO4)solution is added to 30mL of 0.2M(NH4OH) soulution. The .pH of the resultant mixture is : [.pkb of NH4OH=4.7].
View SolutionHow many moles of NH4Cl should be added to 200mL solution of 0.18MNH4OH to have a pH of 9.60.Kb of NH4OH=2×10−5
View SolutionThe pH of 0.02MNH4Cl solution will be : [Given Kb(NH4OH)=10−5andlog2=0.301]
View SolutionThe pH of 0.02MNH4Cl solution will be : [Given Kb(NH4OH)=10−5andlog2=0.301]
View SolutionHow much ml of 0.3MNH4OH should be mixed with 30mL of 0.2M solution of NH4Cl to given buffer solution of pH8.65? (pKb =4.74)
View SolutionSolution of 0.1NNH4OH and 0.1NNH4Cl has pH9.25, then find out pKb of NH4OH.
View SolutionWhat will be pH of 100 ml M10NH4OH+100 ml M10 HCl Solutionat25∘C
(givenKb[NH4OH]=10−5)
View SolutionThe potential of the cell at 25∘C is
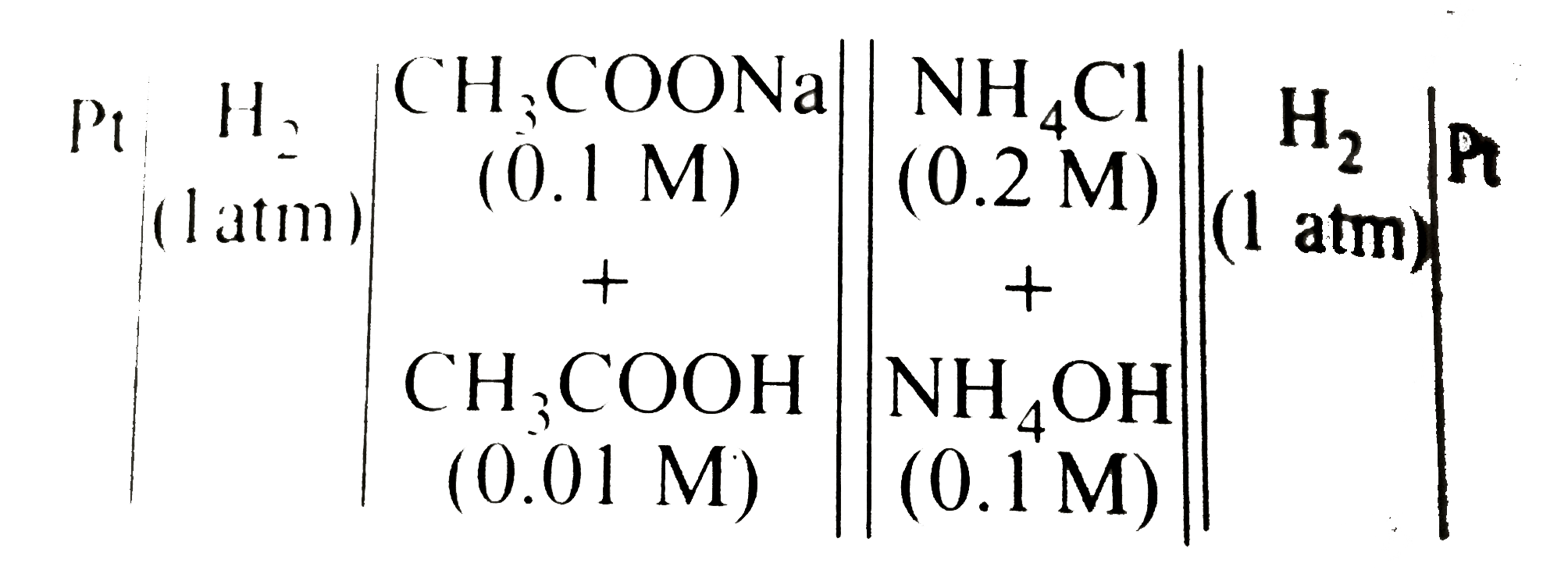
Given pKa of CH3COOH and pKb of NH4OH=4.74
View Solution

