The state S1 is
1s
2s
2p
3s
The correct Answer is:B
To determine the state S1, we can follow these steps:
Step 1: Understand the notation
The notation S1 indicates that we are dealing with an spherically symmetrical state. In atomic orbitals, the "s" refers to the s orbital, which is known for its spherical shape.
Hint: Remember that "s" orbitals are spherical in shape.
Step 2: Identify the possible options
The options given are:
1. 1S
2. 2S
3. 2P
4. 3S
Since S1 refers to an s orbital, we can eliminate option 3 (2P) because P orbitals are not spherical.
Hint: Focus on the options that contain "S" as they represent s orbitals.
Step 3: Determine the number of nodes
The S1 state is said to have one radial node. The number of radial nodes in an orbital can be calculated using the formula:
Number of radial nodes=n−l−1
where n is the principal quantum number and l is the azimuthal quantum number. For s orbitals, l=0.
Hint: Recall that for s orbitals, l is always 0.
Step 4: Apply the formula
For the S1 state:
Number of radial nodes=n−0−1=n−1
Since it is given that there is one radial node, we can set up the equation:
n−1=1
Solving this gives:
n=2
Hint: Solve for n to find the principal quantum number.
Step 5: Identify the correct state
Since we found n=2, this corresponds to the 2s orbital. Thus, the state S1 is 2S.
Hint: Match the value of n to the appropriate orbital designation.
Final Answer
The state S1 is 2S.
The notation S1 indicates that we are dealing with an spherically symmetrical state. In atomic orbitals, the "s" refers to the s orbital, which is known for its spherical shape.
The options given are:
1. 1S
2. 2S
3. 2P
4. 3S
The S1 state is said to have one radial node. The number of radial nodes in an orbital can be calculated using the formula:
Number of radial nodes=n−l−1
where n is the principal quantum number and l is the azimuthal quantum number. For s orbitals, l=0.
For the S1 state:
Number of radial nodes=n−0−1=n−1
Since it is given that there is one radial node, we can set up the equation:
n−1=1
Solving this gives:
n=2
Since we found n=2, this corresponds to the 2s orbital. Thus, the state S1 is 2S.
The state S1 is 2S.
Topper's Solved these Questions
- STRUCTURE OF ATOM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - NCERT EXEMPLAR PROBLEMS
16 Videos
- STRUCTURE OF ATOM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - ASSERTION & REASON
15 Videos
- STRUCTURE OF ATOM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - Assertion And Reason
15 Videos
- STATES OF MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - STATES OF MATTER EXERCISE - Assertion And Reason
15 Videos
- THE P-BLOCK ELEMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THE P-BLOCK ELEMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
The hydrogen -like species Li2+ is in a spherically symmetric state S1 with one node. Upon absorbing light , the ion undergoes transition to a state S2. The state S2 has one radial node and its energy is equal is to the ground state energy of the hydrogen atom.
The sate S1 is
View SolutionThe hydrogen -like species Li2+ is in a spherically sysmmetric state S1 with one node ,Upon ansorbing light , the ion undergoes transition to a state S2 The state s2 has one radial node and its energy is equal is to the ground state energy of the hydrogen atom
The sate S1 is
View Solution
Knowledge Check
The orbital angular momentum quantum number of the state S2 is
A0B1C2D3The energy of state s1 in units of the hydrogen atom ground state energy in
A0.75B1.5C2.25D4.5
The hydrogen -like species Li2+ is in a spherically symmetric state S1 with one node. Upon absorbing light , the ion undergoes transition to a state S2. The state S2 has one radial node and its energy is equal is to the ground state energy of the hydrogen atom.
Energy of the state S1 in units of the hydrogen atom ground state energy is
View SolutionThe hydrogen -like species Li2+ is in a spherically sysmmetric state S1 with one node ,Upon ansorbing light , the ion undergoes transition to a state S2 The state s2 has one radial node and its energy is equal is to the ground state energy of the hydrogen atom
Energy of the state S1 in units of the hydrogen atom ground state enegy is
View SolutionIn given circuit all capacitor were uncharged initially. First switch S1 is closed for long time. When circuit reaches to steady state S1 is opened and S2 closed.

The current through R2 jus after closing the switch S2 is
View SolutionThe hydrogen -like species Li2+ is in a spherically symmetric state S1 with one node. Upon absorbing light , the ion undergoes transition to a state S2. The state S2 has one radial node and its energy is equal is to the ground state energy of the hydrogen atom.
The orbital angular momentum quantum number of the state S2 is
View SolutionIn the given circuit switch S2 is Kept closed and S1 is kept open for a very long time such that the system is in steady- state . Now S1 is also slosed keeping S2 closed.
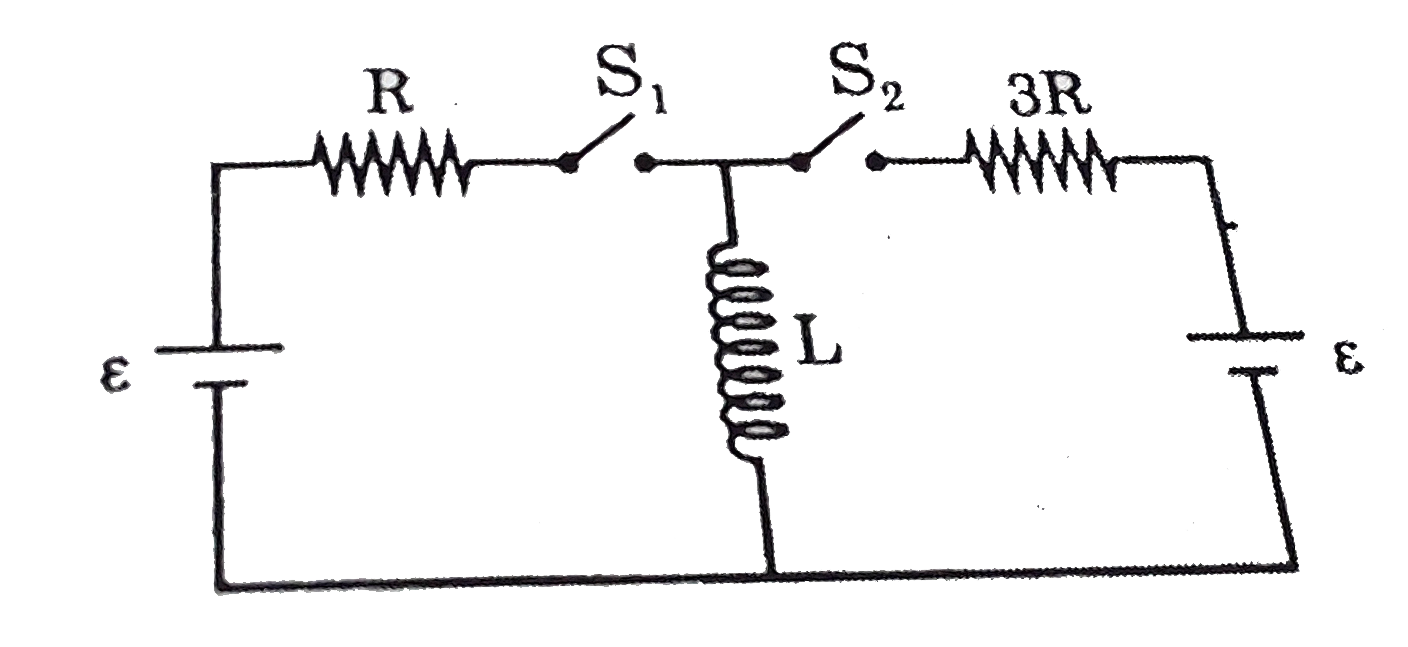
Current passing through R just after S1 is closed , is :
View SolutionIn the given circuit switch S2 is Kept closed and S1 is kept open for a very long time such that the system is in steady- state . Now S1 is also slosed keeping S2 closed.
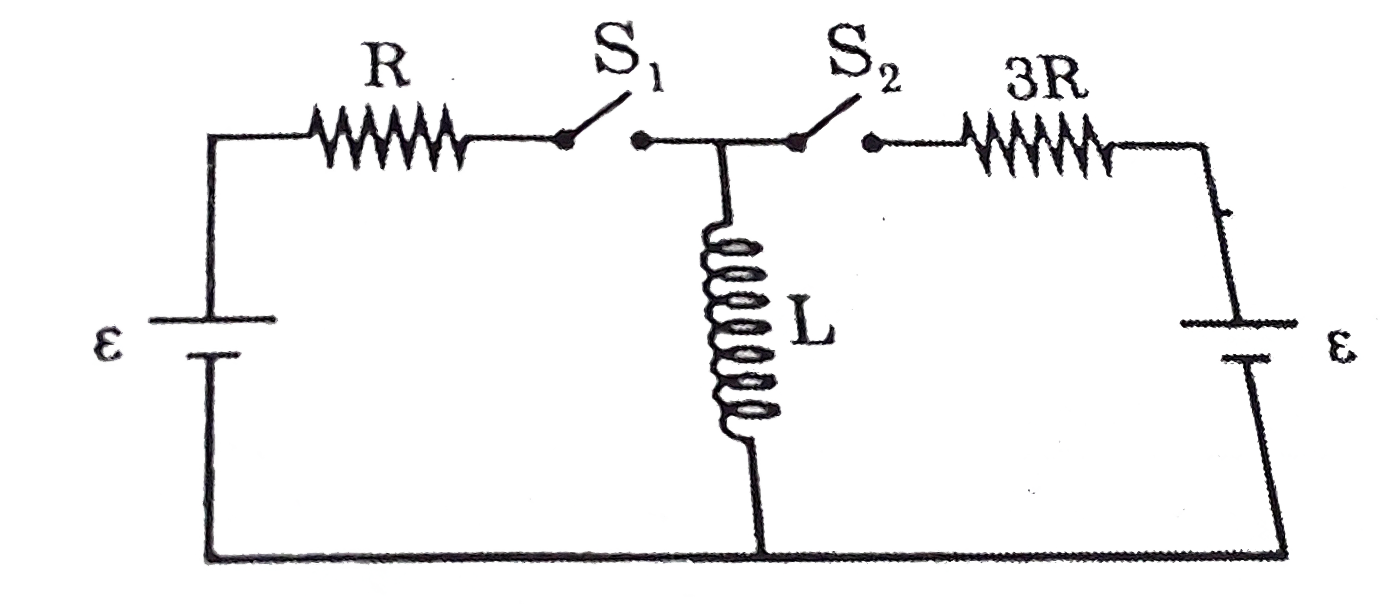
Current passing through inductor L time after S1 is closed , is :
View Solution
