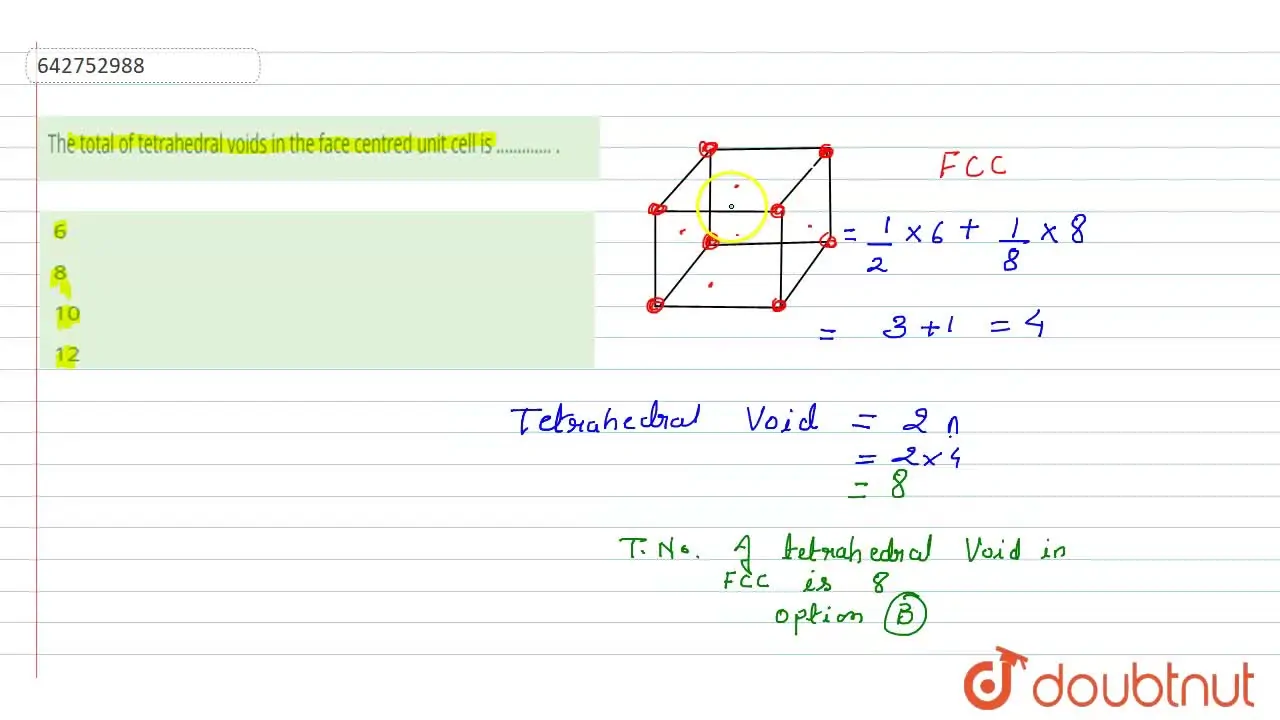
The total of tetrahedral voids in the face centred unit cell is …………. .
6
8
10
12
The correct Answer is:B
No. of atoms per unit cells in face centred unit cell =4
∴ No. of tetrahedral voids = 2 x 4 =8
Related Playlists
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THE SOLID STATE EXERCISE - ASSERTION & REASON15videos
THE SOLID STATE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THE SOLID STATE EXERCISE - Amorphous And Crystalline Solids3videos
THE SOLID STATE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THE SOLID STATE EXERCISE - HOTS7videos
THE SOLID STATE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THE P-BLOCK ELEMENTS EXERCISE - Assertion And Reason15videos
THE P-BLOCK ELEMENTS
Similar Questions
The total number of tetrahedral voids in the face centred unit cell is
View SolutionThe total of tetrahedral and octahedral voids in the face centred unit cell is …………. .
View SolutionThe number of octahedral voids in case of hcp unit cell is
View SolutionThe number of tetrahedral voids in the unit cell of a face centred cubic lattice of similar atoms is
View SolutionA unit cell is obtained by closed packing layers of atoms in ABAB …… pattern. The total number of tetrahedral and octahedral voids in the unit cell are respectively
View Solutionthe number of tetrahedral voids per unit cell in NaCl crystal is ………… .
View SolutionTotal number of octahedral voids present per unit cell of ccp unit cell is
View SolutionThe void space in a primitive unit cell is :
View SolutionIf 'Z' is the number of atoms in the unit cell that represents the closet packing sequence……ABCABC….. The number of tetrahedral voids in the unit cell is equal
View SolutionNumber of tetrahedral voids occupied in a unit cell of diamond is
View Solution