Motion of an oscillating liquid column in a U-tube is
periodic but not simple harmonic.
non-periodic
simple harmonic and time period is independent of the density of the liquid.
simple harmonic and time period is directly proportional to the density of the liquid.
The correct Answer is:C
To solve the question about the motion of an oscillating liquid column in a U-tube, we can follow these steps:
Step 1: Understanding the Motion
The motion of a liquid column in a U-tube can be analyzed by considering the forces acting on the liquid due to gravity and the restoring force that arises when the liquid is displaced from its equilibrium position.
Hint: Consider how the forces change when the liquid is displaced.
Step 2: Identifying the Type of Motion
The oscillation of the liquid column can be classified based on its characteristics. In this case, we need to determine if the motion is periodic and if it can be classified as simple harmonic motion (SHM).
Hint: Recall the definitions of periodic motion and simple harmonic motion.
Step 3: Deriving the Time Period
For a U-tube, the time period T of oscillation can be derived using the formula:
T=2π√hg
where:
- T is the time period,
- h is the height of the liquid column,
- g is the acceleration due to gravity.
Hint: Think about how the height of the liquid column affects the time period.
Step 4: Analyzing the Dependence on Density
From the derived formula, we can see that the time period T does not include the density of the liquid. This means that the time period is independent of the density of the liquid.
Hint: Check if density appears in the formula for time period.
Step 5: Conclusion
Based on the analysis, we can conclude that the motion of the oscillating liquid column in a U-tube is simple harmonic and the time period is independent of the density of the liquid.
Final Answer: The correct option is that the motion is simple harmonic and the time period is independent of the density of the liquid.
Summary of the Steps:
1. Understand the forces acting on the liquid.
2. Identify the type of motion (periodic vs. simple harmonic).
3. Derive the time period using the appropriate formula.
4. Analyze the dependence of the time period on the density.
5. Conclude based on the findings.
The motion of a liquid column in a U-tube can be analyzed by considering the forces acting on the liquid due to gravity and the restoring force that arises when the liquid is displaced from its equilibrium position.
The oscillation of the liquid column can be classified based on its characteristics. In this case, we need to determine if the motion is periodic and if it can be classified as simple harmonic motion (SHM).
For a U-tube, the time period T of oscillation can be derived using the formula:
- T is the time period,
- h is the height of the liquid column,
- g is the acceleration due to gravity.
From the derived formula, we can see that the time period T does not include the density of the liquid. This means that the time period is independent of the density of the liquid.
Based on the analysis, we can conclude that the motion of the oscillating liquid column in a U-tube is simple harmonic and the time period is independent of the density of the liquid.
1. Understand the forces acting on the liquid.
2. Identify the type of motion (periodic vs. simple harmonic).
3. Derive the time period using the appropriate formula.
4. Analyze the dependence of the time period on the density.
5. Conclude based on the findings.
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion & Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Periodic And Oscillatory Motions
7 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Higher Order Thinking Skills
8 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
Which of the following examples represents (nearby) shm and which represents periodic but not shm.
(i) The rotation of earth about its axis.
(ii) Motion of an oscillating mercury column in a U-tube.
(iii) Motion of a ball bearing inside a smooth curved bowl when released from a point slightly above the lowermost position.
(iv) General vibration of a polyatomic molecules about its equilibrium configuration.
View SolutionWhich of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
(a) The rotation of earth about its axis. (b) Motion of an oscillating mercury column in a U tube,
(c) Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most position. (d) General vibrations of a polyatomic molecule about its equilibrium position.
View Solution
Knowledge Check
A capillary tube (A) is dipped in water. Another identical tube (B) is dipped in a soap-water solution. Which of the following shows the relative nature of the liquid columns in the two tubes?
A B
B C
C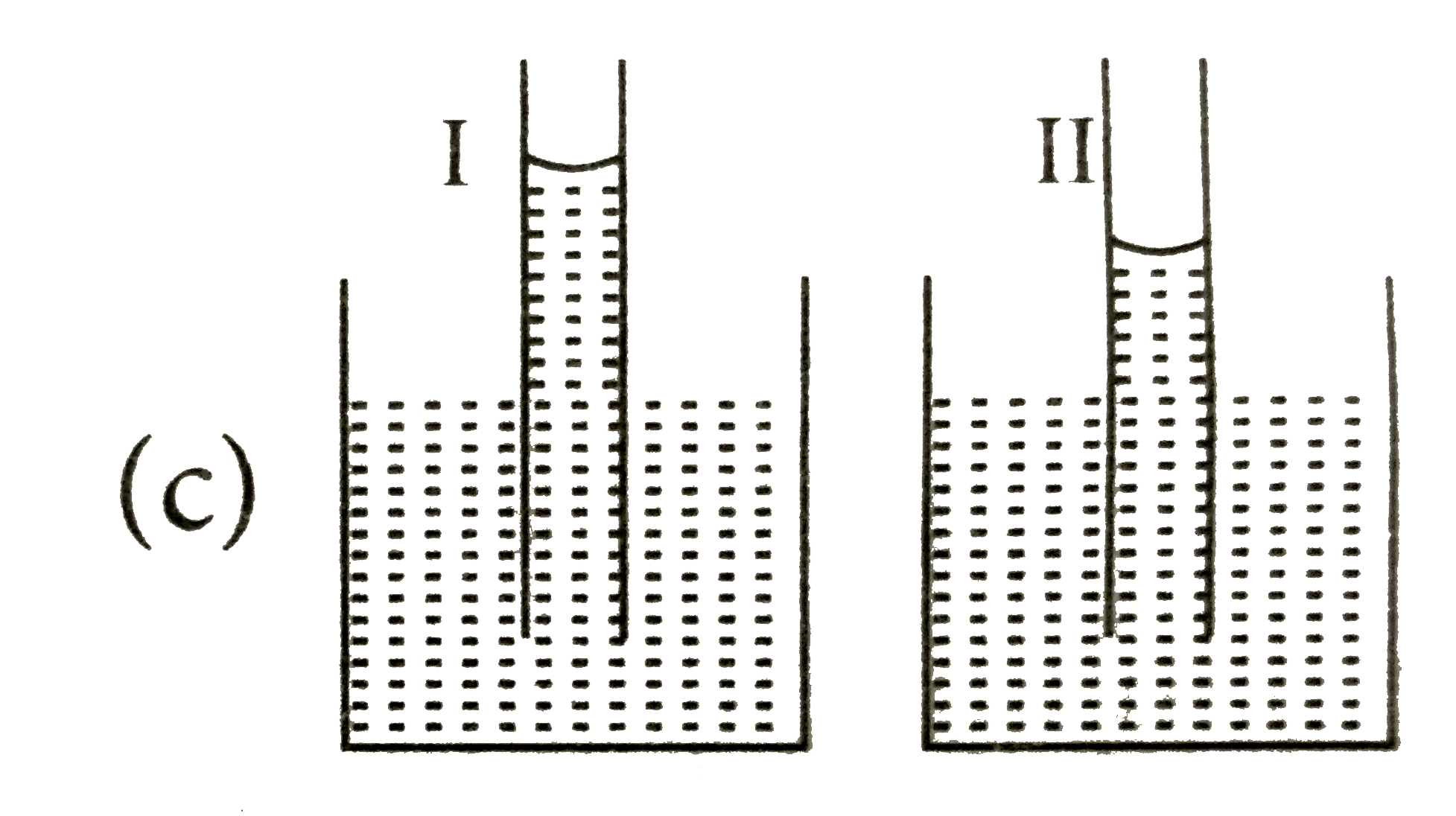 D
D
What is the period of oscillation of a liquid contained in a U - tube executing shm ?
View SolutionThe period of oscillation of a liquid in a U. Tube is one to be T1 The first liquid is replaced by another are of higher density. Will there be any change in the period ?
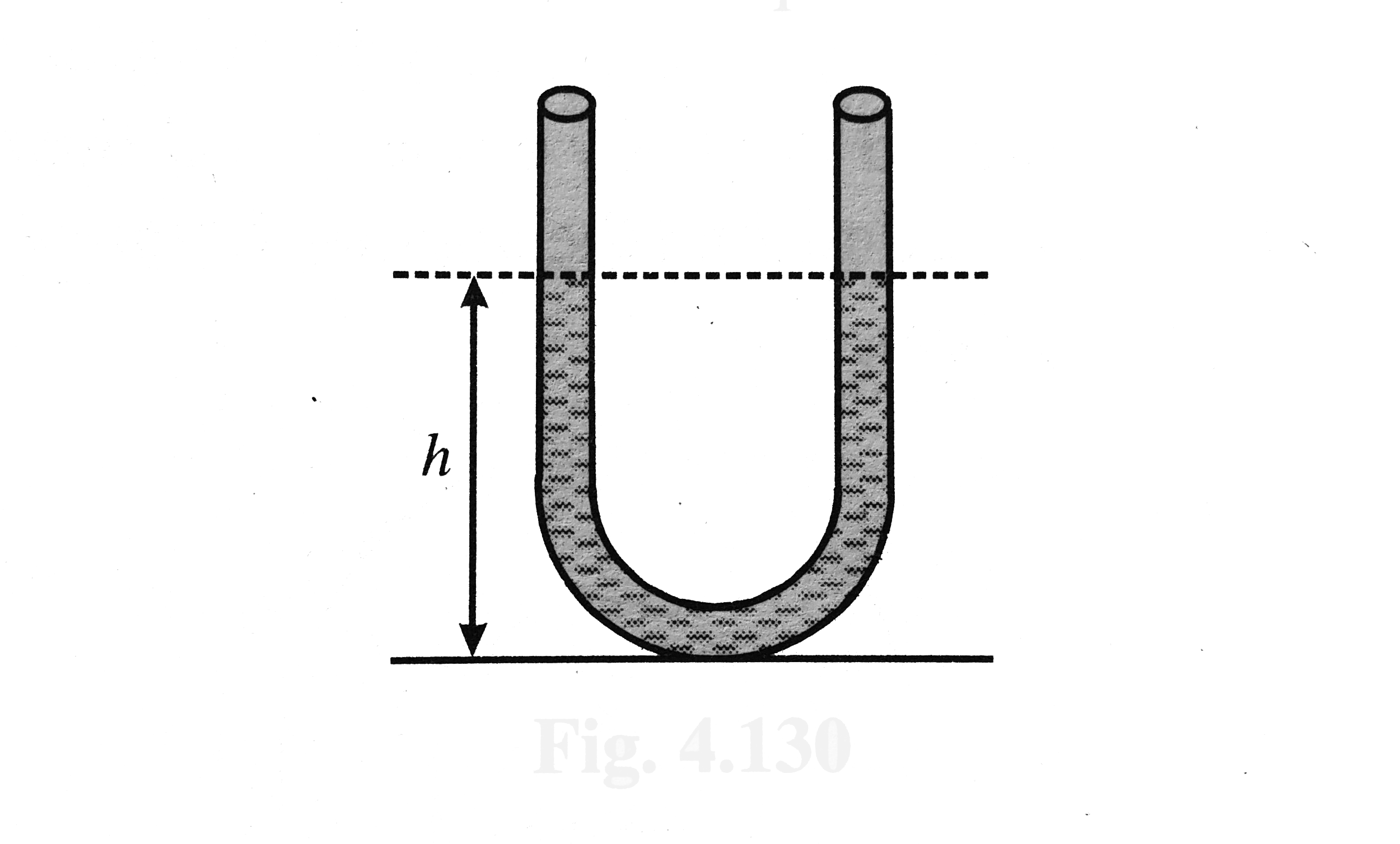
View SolutionConsider a liquid which fills a uniform U - tube uniform U- tube, as shown in figure , up to a height h. Find angular the frequency of small oscillation of th eliquid in the U - tube.
View SolutionA capillary tube is dipped in water to a depth and the water rises to a height h(<l) in the capillary tube. The lower end of the tube is closed in water by putting a lower over it. The tube is now taken out and the thumb is removed from the lower end and it kept open. The length of liquid column in the tube will be

View SolutionA capillary tube (A) is dipped in water. Another identical tube (B) is dipped in a soap-water solution. Which of the following shows the relative nature of the liquid columns in the two tubes?
View SolutionA vertical U−tube contains a liquid. The total length of the liquid column inside the tube is 1. When the liquid is in equilibrium, the liquid surface in one of the arms of the U−tube is pushed down slightly and released. The entire liquid column will undergo a periodic motion.
View SolutionSTATEMENT-1: Time period of the liquid executing S.H.M.in a U-tube depends on the area of cross section of U-tube.
and
STATEMENT-2 : The restoring force acting on liquid displaced from equilibrium position of U -tube depends on the difference in levels of liquid in the two limbs of U -tube.
View Solution
